|
| Laplace et le élo par ni***as***o*1240 le
[Aller à la fin] |
| Actualités | |
De deux choses l’une : une question peut être modélisée statistiquement, ou pas. Dans le premier cas on peut faire des calculs, et tout le monde fini par tomber d’accord. Si par exemple Mr X jette 2n fois une pièce parfaitement équilibrée, et que Mr Y veut parier sur le nombre de piles/faces obtenu, son choix donnant l’espérance de gain maximale est n/n. Dans le second cas, Puch a raison, on ne peut rien prouver de façon scientifique lorsque l’énoncé n’est pas modélisable. Mais cela ne nous empêche pas d’avoir quand même un avis, philosophique disons, sur la question.
Si, dans le même exemple de la pièce qu’on jette 2n fois, on ne sait rien sur l’équilibrage de cette pièce, l’équipe Laplace/PE pense qu’il est "sage" (utilisons ce mot puisqu’on est en dehors du champ scientifique) de continuer de parier sur une dispersion n/n. Cette idéologie me semble contestable puisque l’argument est de dire qu’en présence d’une couille dans le potage, cette couille a autant de chance d’être de gauche que de droite… Bref nos amis utilisent une hypothèse (la pièce a autant de chances d’être déséquilibrée dans un sens que dans l’autre), alors que l’énoncé stipule qu’en fait on ne dispose d’aucune telle hypothèse… Nous avons donc affaire ici à une « profession de foi » qui est que, en l’absence d’information, on fait l’hypothèse d’une information « neutre ».
Ma propre profession de foi, comme je l’ai déjà indiquée via l’exemple de l’enfant extra-terrestre qui apprend les échecs, et sur lequel on veut parier sur son futur élo maximal, est qu’en l’absence d’information, on a autant de chances de gagner en pariant 2000 (ce qu’on aurait fait avec l’information que l’enfant est terrestre), qu’en pariant 10000. Mon crédo est donc qu’en l’absence d’information à la source, on n’a pas non plus d’information à la sortie, donc qu'il est "sage" d'en déduire que tous les paris possibles se valent.
|
|
|
On se retrouve maintenant avec deux fils créés plus un détourné, on reste sur le détourné ? ;)
|
|
|
Il n'y a pas d'accent à elo (Arpad Elo)
|
|
|
Je dirai celui-là, que je me sois pas cassé le cul pour rien en résumant l'histoire !
|
|
|
Donc, imaginons je pose demande à ma grand-mère, qui n'a aucune notion du jeu d'échecs ni du classement utilisé, et qui ignore tout de la langue hongroise (Arpad Elo était-il bien d'origine hongroise? sinon rectifier...), d'orthographier le mot "Elo", sachant qu'il s'agit d'un mot de trois lettres se terminant par un L et un O.
Si elle écrit correctement "elo", succès, le résultat de l'expérience est 1. Si elle échoue en écrivant "élo", échec, le résultat est zéro. admettons qu'elle n'écrive jamais autre chose que l'une de ces deux graphies.
je répète l'expérience avec N grands-mères (disons que je recrute ses amies de son club du 3è âge du village de Noisseville) de façon identique et indépendante.
Mon ami Petiteglise aime beaucoup parier.
Je lui propose donc de miser sur le score final. A-t-il raison de miser sur un score de N/2 ?
|
|
|
Bon, je n'y connais rien en maths Pùch mais, à mon sens, ton exemple est "biaisé". Tu pars du principe que les grand-mères sont "équilibrées" ie qu'elles ne choisissent pas de manière aléatoire.
- elles ont une "expérience" de la langue française
- qu'il y a 18 mots (noms) communs de trois lettres commençant par E, douze ont le "phonème" "ɛ" et "e" (é ou è) et que sur les douze, 8 ont un accent
- que l'effet d'apprentissage fait que la graphie avec un accent sera favorisée (si on ne connaît pas ce bon Arpad)
Je pense donc qu'il faut modifier les conditions initiales en recrutant des grand-mères de langue non latine, ne connaissant pas l'alphabet latin, en leur montrant le texte à trou et les deux possibilités offertes. Dans ce cas là, la prononciation du mot est presqu'accessoire.
Nos grands mères sont alors équilibrées. Peut-être parierais-je sur N/2 moi aussi.
Mais l'expérience me semble inutile.
|
|
|
Non, justement, je ne pars pas d'un principe d'équiprobabilité, un des points que j'essaie d'expliquer à Jo' est qu'on peut choisir "au hasard", de façon "aléatoire", de nombreuses façons différentes sans que cela ne soit ni "biaisé" ni "non-naturel", et que le résultat n'est pas forcément une répartition homogène ou même symétrique.
J'accepte volontiers tes propositions pour améliorer le protocole expérimental. Si j'ai bien suivi, dans "ma" version, tu prends le pari à, disons, 0,4 * N si Jo parie à 0,5 * N ?
Sinon, tout-à-fait d'accord avec ta dernière phrase. Sauf mises considérables, je crois que je vais renoncer à mettre en oeuvre ce protocole expérimental.
|
|
|
Non pùch, ton pari est biaisé, comme l'a dit ce bon vieux Gillou (salutations au passage !)
Car on est dans un cas où l'on a des informations décisives en faveur d'un camp.
Un pari ad hoc serait le suivant :
Imaginons que j'arrive face à toi avec une feuille contenant cette inscription จะม je t'annonce que cette inscription est le mot thaï pour "elo".
(Evidemment, je fais l'hypothèse que tu n'as aucune notion de thaï, si c'est le cas le pari ne marche pas)
Tu vas vouloir chercher des informations pour savoir si je dis vrai ou pas. Tu pourrais en trouver en googlant ou en demandant à une connaissance thaï. Mais si tu ne trouves pas d'info décisive (on est face à face et tu n'as pas google à disposition) qu'est-ce qui te reste ? Des infos oui (tu sais que je te propose le pari, tu peux penser que j'ai pensé à ce que tu allais penser et que donc tu vas dire que je mens mais du coup tu vas penser que je dis la vérité, etc) bref, tes informations n'allant ni dans un sens ni dans l'autre, tu as exactement 50% de chance de trouver la bonne réponse. Et donc si je te laisse une cote, tu dois, rationnellement, prendre le pari.
Et pourtant, j'ai très bien pu fixer la proba que je dise vraie à 1 ou à 0 ou à n'importe quelle proba "générable" comprise entre 1 et 0 (ex en tirant au sort entre 3 feuilles dont 2 contiennent le bon mot et pas la troisième, on a bien une proba de 2/3, etc)
|
|
|
Ce cas entre dans le contexte de la fin de mon post initial : puisqu'on n'a pas d'information à la source, tous les paris se valent. Comme on a 2 paris possibles (ton annonce est vraie ou fausse), j'ai 1 chance sur 2 de gagner quel que soit mon choix.
C'est pareil que si je t'annonce que j'ai déposé une enveloppe chez un notaire contenant un nombre entier de 1 à 10. Si je te demande de parier sur le nombre inscrit, tu as 1 chance sur 10 de gagner quel que soit ton choix, bien que tu ne connaisses pas le protocole que j'ai utilisé pour choisir mon nombre.
Mais en aucun cas tu augmentes ta probabilité de gagner en "centrant" ton choix sur 5 ou 6. Pourtant, si mon protocole est de lancer 100 fois un dés à 10 faces, et de choisir le nombre entier le plus proche de la moyenne obtenue, tu as intérêt à choisir 5 ou 6. Mais le hic est que tu n'as aucune indication qui te permette de croire que j'ai utilisé un tel protocole...
|
|
|
Oui Nico, je n'ai jamais le dit contraire. Mais dans le cas de l'inflation je ne prétendais pas deviner l'inflation exacte, mais donner la meilleure estimation possible avec nos connaissances actuelles.
|
|
|
Edit : j'avais écrit une connerie.
|
|
|
J'ai la flemme de relire en détail les guirlandes, mais il me semble que tu disais qu'en l'absence d'informations sur le taux d'inflation/déflation, il était sage de supposer qu'il était nul. Moi je dis qu'il est sage de supposer qu'il y a autant de chances qu'il soit nul que n'importe quoi d'autre...
Si maintenant tu as des informations, il faut dire lesquelles et, si elles sont suffisamment précises, en déduire une conclusion statistique sur ce taux.
|
|
|
Bah à la question à quel classement elo actuel équivalent les 2785 de Fischer, tu seras d'accord qu'il est plus sage de répondre 2785 que 10 000, ou 1515 non ?
(en contradiction avec ce que tu viens de dire)
|
|
|
Non ce n'est pas contracdire, c'est dû aux fameuses informations cachées dont on a déjà parlé. Par exemple le fait que la fide aurait déjà réagi si le élo actuel de Fischer valait 1515.
Mais dans le cas (théorique) où vraiment on ne dispose d'aucune information, effectivement il est aussi sage de penser que Fischer "vaut" aujourd'hui 1515 que n'importe quel autre classement.
|
|
|
Parce que tu raisonnes dans R alors que R n'existe pas dans le monde qui nous entoure.
Ou alors tu prétends que les règles régissant l'inflation du élo sont un moyen de générer n'importe quel nombre appartenant à l'ensemble des réels, ce qui est évidemment faux.
|
|
|
Mais cela dit, sans faire de la "philo des maths", on peut retomber sur terre et répondre à la question initiale, avec les informations dont tu disposes, tu dirais que Fischer 2785 vaut quel classement actuel ?
|
|
|
Je ne dispose d'aucune information suffisamment fiable pour pouvoir répondre à cette question. Au feeling je dirais assez nettement moins, vu la progression générale de la qualité de jeu. Par exemple Carl Lewis (avec son meilleur temps de l'époque) ne serait même pas qualifié aujourd'hui dans une finale mondiale du 100m...
Mais pour en revenir à nos moutons, tu remarqueras que dans un modèle à 2 joueurs, avec la victoire à 3 points, la nulle à 1 et la défaite à 0, l'inflation tend vers + l'infini lorsque le nombre de parties non nulles tend vers + l'infini. Il est donc tout à fait possible (théoriquement parlant) que l'inflation soit n'importe quel réel.
|
|
|
Ton avis, qui est loin d'être bête bien qu'on ne peut se baser sur ce seul critère, est loin d'être le plus commun, en tous cas ici !
|
|
|
Je pense qu'il n'est pas impossible de démontrer qu'il y a inflation du à l'abaissement du seuil d'entrée. En revanche il est quasi impossible de démontrer qu'un joueur est plus ou moins fort qu'un autre à deux époques différentes. Que le niveau (force+ conditions) soit plus élevé oui, que le joueur soit plus fort, non.
|
|
|
deux phrases:
"Mais dans le cas de l'inflation je ne prétendais pas deviner l'inflation exacte, mais donner la meilleure estimation possible avec nos connaissances actuelles."
Visiblement tu te contrefiches de nos connaissances actuelles du système elo (sans doute très incomplètes mais toujours meilleures que celles de ma grand-mère en hongrois), puisque tu te limites à un cas hyper théorique où on ne saurait rien de rien. Et de plus tu ne cherches pas à estimer la supposée inflation, mais juste à gagner un pari, ce qui n'est pas du tout la même chose intellectuellement parlant.
"Parce que tu raisonnes dans R alors que R n'existe pas dans le monde qui nous entoure."
R est l'initiale pour "réel". J'ai bien compris que tu prends en compte les limites de notre imagination et de la mémoire de nos ordinateurs, mais tout de même, n'insultons pas le Monde !
|
|
|
Au début du premier fil, beaucoup disaient que Fischer 2785 vaut bien plus actuellement (disons 2900), Nico dit l'inverse (disons 2700, Nico corrigera s'il le veut). Tu dis quoi Pùch ?
|
|
|
Et sinon, pour le problème thaï, tu es d'accord pour dire que tu as une chance sur deux (ne cherche pas à biaiser le problème ou l'éviter en me disant que tu cherches sur google ou autre...)
|
|
|
"Carl Lewis (avec son meilleur temps de l'époque) ne serait même pas qualifié aujourd'hui dans une finale mondiale du 100m..."
Carl Lewis a fait 9''86. Sans être un expert ça m'étonnerait qu'on ne se qualifie pas pour une finale avec ça.
|
|
|
Je dirais à peu près 2700 aussi. Ce qui n'ôte rien au talent de Fischer, s'il pouvait jouer aujourd'hui avec sa forme de 1970 il ferait certainement d'énormes progrès et se retrouverait dans les tout premiers mondiaux (grâce à une forte opposition, au développement la théorie, à l'utilisation de logiciels pour s'entraîner, etc...).
Mais même en supposant que j'aie raison et que le niveau de Fischer en 1972 corresponde à 2700 dans l'évaluation actuelle, cela ne prouverait en rien une "déflation" (terme qui reste à définir pour une transformée d'applications). On pourrait imaginer que l'évaluation elo ait changé de sorte que, par exemple:
2785 (elo 1972) == 2700 (elo 2012)
2400 (elo 1972) == 2520 (elo 2012)
2210 (elo 1972) == 2080 (elo 2012)
NC (elo 1972) == NC ou entre 1001 et 2120 (elo 2012).
Ou d'autres valeurs bien sûr. Dans ce cas, doit-on parler d'inflation ou de déflation ?
Cela ne sera possible que si on applique une mesure à l'ensemble des niveaux de jeu.
|
|
|
Pour ton problème Thaï, je te l'ai accordé une bonne dizaine de fois. Tu peux aussi dire que tu jettes une pièce.
C'est juste un résultat trivial sans aucune portée concernant l'évaluation Elo.
|
|
|
Il me semble qu'il y a en fait 2 questions distinctes :
- Soit on téléporte le Fischer de 25 ans aujourd'hui et on calcule son nouvel élo.
- Soit on fait renaître Fischer il y a 25 ans, et on regarde son élo aujourd'hui.
Les résultats seraient, de mon point de vue, très différents. S'il faut absolument donner des nombres, disons 2650 et 2850.
Pour dire les choses autrement, le génie est universel mais la performance ne l'est pas...
|
|
|
Oups croisement avec Puch. Oui elkine, l'exemple choisi n'est certainement pas le meilleur, je change avec celui de Mark Spitz ! De toutes manières on voit l'idée...
|
|
|
Le "problème thaï" on en a déjà parlé : si tu as le droit de choisir entre les deux réponses, tu choisis au hasard entre p et 1-p et ça donne 1/2.
nico : certes, je vois l'idée.
|
|
|
Fischer, s'il pouvait jouer aujourd'hui avec sa forme de 1970 opposerait à son adversaire non seulement son Elo mais aussi sa présence physique et sa profonde connaissance du jeu.
Il y a fort à parier qu'il pourrait affronter sans crainte n'importe quel super-GMI actuel
|
|
|
Etant plutôt connaisseur en athlétisme, je confirme que Lewis serait en finale sans aucun problème et pas loin du podium avec 9"86. Même Jesse Owens serait assez proche de la finale , d'autant que rien que sur la qualité de la piste il gagne un dixième facile par rapport à la cendrée.
Spitz est un meilleur exemple en effet.
|
|
|
Pour Fischer on spécule totalement mais dans quelles conditions on l'amène ? On lui file les parties récentes ? Parce qu'en 1970 il disposait de la même information théorique que ses concurrents, les parties étaient moins diffusées mais il avait accès à la littérature et aux revues disponibles.
Pourquoi alors qu'une de ses forces était d'être un des joueurs les mieux préparés de son temps on lui enlèverait arbitrairement cet avantage ?
Enfin ça me semble relativement insoluble dans le domaine de l'ouverture au sens large. Soit on le handicape terriblement soit on change radicalement son niveau de jeu en lui attribuant un niveau de connaissance analogue à celui qu'il avait à l'époque, mais comment évaluer ça ?
PS : si on fait renaître Fischer il y a 25 ans il est peut-être à Guantanamo à l'heure qu'il est !
|
|
|
Oui, faire revenir Fischer, en plus d'un scénario médiocre pour film de science-fiction, se heurte à pas mal de difficultés pratiques. C'est pourquoi je pense qu'on doit considérer non pas le joueur mais le niveau du joueur, c'est-à-dire Fischer avec sa forme de 1972, ses connaissances de 1972, ni plus ni moins.
Je pense que c'est ce que Nico voulait dire avec sa première hypothèse "on téléporte Fischer".
L'avantage c'est qu'on a une donnée objective (bien qu'incomplète) pour évaluer le niveau de Fischer: les coups et les parties qu'il a joués.
|
|
|
d'accord avec le post précédent de puch puisque l'amélioration de la préparation a amené une élévation du niveau (au moins dans ce secteur) et qu'on essaie de savoir si le elo permet comparer les niveaux à travers les âges et non la force. Mais plutôt que téléporter Fischer qui est une expérience de la pensée, on pourrait plutôt se baser sur des logiciels d'échecs de référence.
A noter que le classement elo n'étant pas inflationniste par essence mais plutôt par quelques biais (s'il l'est ce qui reste à prouver car dans le principe et en pratique pour l'essentiel c'est à somme nulle), on peut supposer que l'augmentation (à prouver) du niveau moyen n'a pas pour conséquence une augmentation du elo moyen.
En effet, si j'augmente d'un coup de baguette magique la compréhension du jeu de tous les joueurs d'échecs (par exemple, clin d'oeil aux finalistes, si je suppose que tout le monde connait tour+fou contre tour), le elo moyen restera le même mais le niveau aura augmenté.
On peut supposer de même que les différentes couches de connaissance qui se sont ajoutées depuis Fischer (ouvertures plus pointues et jeu plus pratique en particulier) n'ont pas généré d'augmentation générale de points elo.
|
|
|
D'accord en tout point avec dan31.
|
|
|
J'entends bien, mais il rencontrait des adversaires qui avaient également des connaissances de 72, là c'est à peu près comme si on organisait un tournoi de modules en débranchant la bibliothèques d'ouvertures d'un seul.
Mettons que Fischer joue une Najdorf, on lui plante une "nouveauté" de 1990, que va t'il trouver sur l'échiquier ? Peut-être les meilleurs coups, mais si en face on lui récite 28 coups a tempo et qu'il finit par être en zeitnot est-ce que ça sera vraiment significatif d'un niveau, c'est discutable. Est-ce que ça a du sens de le comparer à des joueurs tous mieux préparés que lui alors que la très bonne préparation faisait partie de sa force ?
Et puis bon, une partie c'est aussi un affrontement, même si Fischer croyait plus aux bons coups qu'à la psychologie il y a tout de même un contexte, une pression, des styles antagonistes, des préparations spécifiques ... Le classement témoigne des résultats, une petite variation de niveau peut avoir une grande incidence, des aspects comme la confiance sont inquantifiables ...
|
|
|
sinon sur le site de la Fide on peut consulter la moyenne Elo du Top 100 mondial...
|
|
|
Sur le principe je suis d'accord mais les joueurs qui connaissaient déjà la finale baisseront un peu relativement aux autres !
Pour les logiciels en 1970 c'était embryonnaire donc il n'a pas été possible de les comparer aux meilleurs de l'époque, on pourrait le faire maintenant (en gardant sous le coude quelques PC pourris pour pouvoir recréer les mêmes conditions) mais ça n'est pas rétroactif hélas, ce serait d'ailleurs intéressant (ça existe peut-être plus ou moins ?!).
Pas sûr que l'on puisse en tirer des conclusions sur le passé ceci dit, je pense que l'abaissement progressif du seuil en particulier est une des principales causes possibles de biais.
|
|
|
c'est pas con , par ex on refait jouer carlsen contre deep blue de l'époque , et on compare avec les résultats de kasparov
|
|
|
dans le même genre on pourrait faire jouer plusieurs logiciels sur le circuit qui affronterait une panoplie de joueurs ayant un classement elo , et ces logiciels ayant eu une estimation elo de l'époque actuelle pourraient reservir dans le futur pour tester si il y a une inflation , stabilité ou déflation du elo , car la force du logiciel resterait elle la même
|
|
|
Heu, pour les logiciels, j'envisageais quelque chose de très différent.
Je mouline toutes les parties de Fischer à cadence lente sur une période donnée avec un très fort logiciel actuel (Houdini, c'est toujours celui-là qui est censé être le plus fort ?). Je lui attribue une note en fonction du nombre de coups qui en sont pas les meilleurs (pour l'ordi), de ceux qui ne sont pas dans les trois meilleurs, de l'importance de l'erreur jouée (si l'évaluation descend de 0.15 ou si elle plonge de 3 points). Ce n'est pas un outil parfait bien qu'on puisse l'améliorer à la marge (gérer les coups d'ouverture, écarter les positions complètement gagnantes ou perdues sauf énorme gaffe, etc...).
J'obtiens une note "Fischer 1970"
Je fais de même pour créer des notes "Kasparov 1988", "Lautier 1996", Petiteglise 2006", "Carlsen 2011", etc...
Si Fischer 1970 a obtenu la même note que Leko 2009, je peux comparer les classements de l'un et l'autre à la fin des années considérées, ou encore leurs performances elo sur lesdites années.
En fait cela sera surtout intéressant pour des niveaux où on des joueurs plus nombreux. Si j'ai 15 joueurs en 2012 et 15 joueurs en 1980 qui obtiennent pratiquement la même note au test Houdini, la comparaison me donnera une indication sur la déformation de l'évaluation elo pour ce niveau donné.
Le tout écrit à la première personne, mais ce n'est pas moi qui m'y colle.
|
|
|
ben t'as des pos ou des types à 2000 peuvent trouver les 20 premiers coups de rybka , d'autres ou les premiers coups sont inhumains , des parties ou les 2 types décident de réciter 30 coups de théorie et de conclure la nulle au 31 eme , alors qu'ils ont tous les 2 un classement médiocre , le style de jeu change aussi , le style d'aujourd'hui ( ou tout est assisté par ordi ) est assez différent de celui de l'époque de morphy
|
|
|
Oui, la notation-Houdini n'est pas un outil parfait. Petrossian sera relativement mieux noté que Tal car il gaffait moins souvent, et pour cause, il jouait des positions plus fermée où il y a beaucoup de coups qui ne feront pas hurler l'ordi, alors que dans un grand binz' tactique même des grands maîtres peuvent passer de +3 à -2 plusieurs fois dans la partie.
Mais si j'ai un grand échantillon de joueurs qui ont la même note-Houdini, ces effets se compensent statistiquement et je peux regarder si ces joueurs obtiennent des classements Elo similaires ou non selon les époques.
|
|
|
cette approche que tu cites puch a été réalisée avec ... crafty pour comparer les champions du monde à travers les âges. Article dont a parlé le site chessbase et je pense que ça a donné lieu à une publication scientifique.
Problème : ça aurait été intéressant pour des joueurs à 2000 mais pas des champions du monde, car crafty ne peut pas juger des coups d'un tel niveau de joueur.
Autre biais : ce que tu dis sur Tal - Petrossian est très juste. Si on étudie un échantillon de joueurs lambda, ce biais n'intervient pas , mais on ne peut pas comparer les champions du monde ainsi, ni même avec houdini. Tal jouait délibérément des coups dont il ne connaissait pas la correction en disant que du point de vue pratique, ça n'avait pas d'importance, car lui ferait moins d'erreur que son adversaire dans les positions résultantes. Cette approche reste judicieuse aujourd'hui, mais la note houdini risquerait d'être sévère pour une telle façon de jouer. Par contre, toujours d'accord avec puch, on pourrait comparer un groupe de 30 (100 ?) joueurs à 2500-2600 de 1980 et de maintenant sans trop de problèmes avec houdini, puisque les effets de style se compenserait sur un nombre assez important de joueurs (qui s'y colle ?).
En réalité, l'approche à laquelle je pensais ressemblait plutôt à celle évoquée par elpancho (même si celle de puch me plait mieux finalement et semble plus faisable) : dans les années 80, des modules comme Mephisto ont été évalués en jouant contre des dizaines d'adversaires aux environs de 2000, ce qui fait qu'on avait une idée correcte de leur elo de l'époque. Retrouvons ces vieilles machines et faisons le même test pour voir leur elo aujourd'hui. Ca nous donnerait la valeur de l'inflation/déflation. OK c'est pas évident en pratique (j'ai moi-même un vieux MM6 en état de marche et je me vois mal organiser 100 parties pour évaluer son elo), mais faisable pour un passionné ! On pourrait imaginer comme elcave utiliser des PC de l'époque et des programmes entre 2000 et 2400 elo. Quant à Deep Blue, helas il a joué trop peu de parties pour que ce soit statistiquement significatif.
|
|
|
Mais comme dit Elpancho le style de jeu change, au 19e tu avais plus de Tals que de Petrossian...
|
|
|
@elkine : d'une part, il me semble qu'on essaie de trouver l'inflation du classement elo sur une période restreinte à disons 30 ans (et même à mon sens plus restreinte, par exemple 10 ans pour commencer). On ne cherche pas à évaluer les classements elo du 19 e siècle. D'autre part le changement global de style de jeu fait partie de l'amélioration du niveau de jeu.
Pour ces raisons à mon avis le biais que tu soulèves est sans doute assez faible pour les méthodes que nous proposons, mais en effet il faut l'avoir en tête. On pourrait imaginer que les joueurs d'aujourd'hui, jouant plus "pratique", prennent plus de risques que les joueurs des années 70-80 et que cela fait baisser leur note houdini.
Il est clair que la méthode la moins biaisée est d'avoir une évaluation elo du même programme (évalué contre des humains) il y a 30, 20 et/ou 10 ans et aujourd'hui, mais est-ce faisable ?
|
|
|
Mettons que tu trouves, dans les années 70-80, un max de parties paisibles à la Spasski, avec très peu d'erreurs. Tu prendrais ça pour une régression du niveau ?
(Croisement avec ton 2e paragraphe.)
|
|
|
non, c'est ce que je dis du reste à la fin de mon 2e paragraphe, pour souligner la pertinence de ta remarque.
Et c'est pourquoi je pense qu'il faut se baser sur une période de 10 ans voire plus court.
EDIT : vu pour le croisement. Donc comparer le niveau de jeu de 30 joueurs aux environs de 2600 en 1990 à celui de 30 joueurs aux environs de 2600 en 2000 : au boulot ! (ou 2000 et 2010).
|
|
|
Sinon, je me cite sur un autre fil juste avant la barre des 200 commentaires :
"Je remarque que l'écart entre le 30e mondial et le 100e mondial (typiquement 60 points) et l'écart entre le 100 e mondial et le 200e mondial (typiquement 40 points) reste très stable depuis 1980. Un argument contre la densification du niveau ? "
J'avoue que ce constat m'a surpris.
Je me pose du coup la question suivante, qu'une petite résolution numérique pourrait éclairer : je pars d'une certaine répartition fixée de joueurs dans le classement elo (disons celle des 200 premiers en 1980). Admettons qu'ils soient classés entre 2450 et 2750. Je double d'un seul coup le nombre de joueurs (multiplie la densité par deux) : j'ai 400 joueurs classés entre 2450 et 2750. Je simule des parties à l'intérieur de cette population en faisant évoluer le elo. Intuitivement, la répartition de elo va se clairsemer à mesure que le temps avance. Par exemple, au buot de 10 000 parties on aura 400 joueurs classés entre 2400 et 2800. Qu'en déduire par rapport au phénomène qui nous intéresse ? Les meilleurs ont-ils progressé ? Difficile question. On pourrait être tenté de dire que l'étalement est purement statistique et pas une question de niveau. Mais un argument inverse dirait qu'un joueur qui passe de 2450 à 2400 finit par se décourager, affronter des joueurs moins forts et "valoir" réellement 2400.
|
|
|
Je pense qu'un biais important est que des joueurs aux classements voisins ont tendance à jouer ensemble.
Même dans le cas où tous les joueurs ont le même niveau constant (26), les fluctuations vont porter certains à 27. Si on augmente le nombre de joueurs, les 27 vont se jouer entre eux et on verra apparaître des 28.
|
|
|
Put... mais quel fil de tordus ;-))
|
|
|
L'autre problème de sortir une population en circuit fermé comme ça, c'est que ça ne correspond plus à la réalité de ce qui se passe.
En pratique effectivement les joueurs qui sont plutôt sur une phase descendante baissent progressivement jusqu'à sortir de la fourchette initiale, mais en pratique ils sont remplacés dans les 200 premiers par des joueurs qui sont eux en ascension.
A vue de nez j'évaluerais le turn-over aux environs de 5% entre deux classements, avec parfois des allers-retours liés à des variations de forme mais globalement pour aboutir à une liste de 200 joueurs je pense qu'il y a un solde légèrement positif par rapport au reste de la population, d'une part liée à l'augmentation graduelle du plancher, d'autre part parce que quelques joueurs qui ont gagné des points remplacent d'autres qui sont stables ou en ont perdu.
D'où d'ailleurs la hausse flagrante du plancher pour figurer dans le top 100 ou 200, plus de cent points depuis que le classement existe. Dans l'exemple les joueurs descendus à 2400 auraient été progressivement remplacés au sein de l'élite par des joueurs initialement à 2350 ou 2400 mais en progression, l'expérience ne le fera pas apparaitre.
|
|
|
@elcave : je suis d'accord, en circuit fermé, ça ne modélise pas bien, mais c'est juste pour se rendre compte de l'effet de la densification.
Comment expliquer que, bien que la densité de forts joueurs nous paraît augmenter (intuitivement), en réalité il y a toujours le même écart elo entre le 200 e et le 100 e qu'il y a 30 ans ? Et entre le 100 e et le 30 e ?
Est-ce qu'en réalité, le nombre de forts joueurs n'augmente pas, ou bien cette augmentation crée-t-elle ex-nihilo par effet statistique (variabilité plus importante des classements par exemple), une dilatation des classements elo qui ne correspondrait plus tout à fait à l'écart des niveaux ?
|
|
|
C'est pas si étonnant. Là où tu avais trois 27 et trente 26, tu as maintenant trois 28 et trente 27 (et un tas de 26). Comme je disais cet élargissement de la base peut se produire même sans augmentation de niveau.
|
|
|
Il y a un aspect qui me semble ne pas encore avoir été évoqué jusqu'à présent, celui des tournois fermés.
En gros en dessous de 2500 les joueurs participent en grande majorité à des opens, avec donc un brassage régulier par rapport à ceux qui sont moins bien classés, on peut considérer que grosso modo les pourcentages déterminés par Elo s'appliquent assez bien (bien sûr il y a toujours des joueurs qui montent et d'autres qui baissent mais le classement est régulièrement mis à l'épreuve des faits et d'une sorte de calibrage).
Ensuite il y a une plage entre disons 2500 et 2700 où les joueurs participent à des tournois fermés, des opens, et des opens qui leur sont réservés, ce qui s'apparente un peu à des tournois fermés pour le problème qui nous occupe.
Enfin il y a l'élite mondiale (disons 27+) qui ne rencontre quasiment pas de joueurs de la première sorte et joue essentiellement entre elle, une sorte de "première division".
Pour les joueurs brassés régulièrement il y a un système qui doit assez bien cadrer avec la loi statistique qui a servi de base, donc tous les 100 joueurs à plus de 2200 mettons il y aura peut-être 10 à plus de 2400 et un à 2600.
Par contre, le joueur qui parvient en haut de cette pyramide "change de division" et se retrouve confronté au microcosme de l'élite, avec éventuellement un sas intermédiaire.
Les deux catégories communiquent à la marge, ceux dont le style ne passe pas face aux meilleurs redescendent un peu et naviguent dans la deuxième catégorie, les joueurs sur la phase descendante peuvent aussi en sortir définitivement, a contrario certains nouveaux venus s'y font une place.
Cette "première division" marche plus ou moins en circuit fermé et fait l'objet d'une hiérarchie interne, sa borne inférieure étant déterminée par le solde entre joueurs qui la quittent, joueurs à la marge et nouveaux venus.
Les variations y sont plus lentes, comme tout microcosme il y a des effets liés à l'habitude (préparations, joueurs qui vous réussissent plus ou moins bien ...).
Le seuil monte à peu près régulièrement il me semble, par contre la répartition au sein de cette "première division" est moins liés à l'aspect statistique je crois, et plus on approche du sommet plus c'est vrai.
|
|
|
C'est un peu ce que j'évoquais "les joueurs aux classements voisins ont tendance à jouer ensemble" mais oui ça semble encore plus vrai en haut de l'échelle.
D'ailleurs à l'époque où je jouais sur ICC il y avait deux classements, le blitz et le "5-minute" aux appariements plus ou moins aléatoires. Ce dernier était beaucoup moins inflationniste.
|
|
|
En général, pour limiter les effets de bord, et pour être sûr d'avoir des échantillons consistants, je pense qu'une première étude ferait mieux de considérer des joueurs forts mais loin de l'élite, du genre autour de 2450.
Selon les résultats, on pourra étendre les recherches ensuite à d'autres niveaux, pour la méthode doit être testée à ce type d'échelon avant d'aborder les tout meilleurs mondiaux. Même si c'est pour eux que l'on aura le plus de curiosité ("Spassky était-il aussi fort qu'Anand ?").
|
|
|
En ce qui concerne les comparaisons entre les époques, je vous transmets un résumé du chapitre que John Nunn y consacre dans son livre "John Nunn's Chess Puzzle Book" (2009).
Ce n'est pas exactement une comparaison de Elo, puisque Nunn recule assez loin, jusqu'en 1911. Il explique comment il fait pour estimer le niveau de jeu d'alors.
p.66 : L’épreuve du temps
Comment comparer les grands maîtres du passé avec les meilleurs joueurs actuels ?
L’approche la plus simple consiste à prendre une très grande base de parties. On considère alors qu’il s’agit d’un seul tournoi gigantesque qui est rejoué indéfiniment. Si on fait ce calcul avec la MegaBase, on aboutit à un résultat plutôt surprenant : après stabilisation, les joueurs modernes sont aux premières places, alors que les « anciens » sont derrière.
A priori cette méthode semble fiable, mais, réflexion faite, ce n’est pas si simple.
Tout d’abord, la sélection de parties. Les données concernant les joueurs récents sont beaucoup plus complètes et détaillées, alors que celles des joueurs d’autrefois sont moins représentatives (moins de parties, présence de parties « parasites » car non-officielles, …)
De plus, on ne détectera pas forcément une éventuelle hausse de niveau, vu que les joueurs ont rencontré des contemporains. Et il faudrait tenir compte de l’évolution de carrière d’un joueur : l’ascension, un certain temps aux alentours de sa force maximale, puis un déclin progressif (sauf que les champions actuels ne sont pas concernés par ce déclin).
Moi, je m’intéresse à l’évolution de la force des joueurs depuis la Première Guerre Mondiale, et je vais employer une autre méthode : l’analyse des parties. Bien que plus subjective, cette approche permet une comparaison directe, valable quel que soit le laps de temps considéré.
On pourrait faire un travail très sérieux là-dessus, mais dans le cadre de ce livre (livre d’exercices), mon propos sera plus limité.
J’ai décidé de prendre deux tournois très espacés dans le temps et d’analyser toutes leurs parties. Et comme je veux quand même pas mal de parties, j’ai pris deux « gros » tournois.
Le tournoi « des temps anciens » est Karlsbad 1911 (26 joueurs en toutes rondes, 325 parties) intéressant pour son mélange de grands champions (Alekhine, Nimzowitsch, Schlechter, Rubinstein) et de noms moins connus (genre Perlis, Fahrni, …). Teichmann l’avait emporté (18/25) devant Rubinstein et Schlechter (17).
Le tournoi récent est l’Interzonal de Bienne 1993 (open de 73 joueurs en 13 parties, 468 parties), avec aussi bien Anand et Kramnik que Gluckman et Kalesis.
C’est Guelfand qui avait gagné (9/13) devant 8 joueurs à 8,5, dont Lautier, Adams, Kramnik …
Pour examiner tout ça, je me suis basé sur la recherche de gaffes, en me disant que c’était un bon moyen d’éliminer les différences résultant de 80 ans de théorie (si on donne une pièce, ce n’est pas parce qu’on ne connaissait pas les théories de Nimzowitsch sur les chaînes de pions).
Dans un premier temps (pour en gagner, justement), j’ai laissé Fritz faire une pré-analyse en mode « graves erreurs ». Il m’a sélectionné une série de coups que j’ai ensuite vérifiés « à la main » pour m’assurer qu’il s’agissait bien de gaffes.
Je n’avais pas d’idées préconçues sur les résultats, et je n’ai pas été déçu : en gros, les joueurs du passé sont bien plus mauvais que ce à quoi je m’attendais. Les gaffes répertoriées étaient si énormes que j’ai regardé beaucoup de parties entières pour voir si elles reflétaient vraiment le niveau de jeu. Et bien oui.
En comparaison, la recherche équivalente pour Bienne 1993 a révélé peu d’horreurs. J’avais prévu au départ de présenter des positions des deux tournois dans ce chapitre, mais c’était si déséquilibré que je me suis concentré sur Karlsbad. J’ai gardé Bienne pour d’autres endroits du livre.
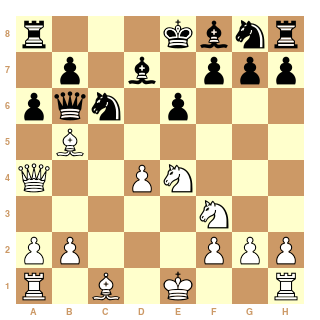
Pour être encore plus précis sur Karlsbad, il n’y a qu’à voir un joueur en particulier : Hugo Süchting (1874-1916). A Karlsbad, il a marqué 11,5/25, soit « moins deux » comme disent les jeunes ; un score tout à fait respectable. Pour avoir rejoué toutes ses parties de Karlsbad, je peux affirmer en toute confiance qu’il ne valait pas plus de 2100 Elo (dans un bon jour et vent dans le dos).
Un exemple de son jeu, face à Alekhine : 10.0-0 ?? Dxb5
|
|
|
Concernant le niveau possible-actuel-science-fiction de Fischer, il me vient une remarque, que je tire de cette déclaration de Yannick Pelletier dans Europe-Echecs n°536 (septembre 2004) :
« Beaucoup de joueurs à 2600 aiment propager la théorie que rien ne les sépare des grands-maîtres à 2700, excepté la préparation dans les ouvertures. A mon avis, rien n’est plus faux. La supériorité d’un super-GMI se reflète dans tous les compartiments du jeu. Ses connaissances échiquéennes sont plus vastes, sa capacité de calcul meilleure, et il est également capable de prendre d’excellentes décisions dans les positions critiques. »
Appliquée au "cas Fischer", cette citation sous-entendrait que les qualités qui avaient permis au champion américain de tant dominer ses adversaires resteraient valides après voyage dans le temps.
On aurait donc un Fischer qui vaudrait bien aujourd'hui ses 2785 anciens (avant même le moindre rattrapage théorique).
|
|
|
@atms : intéressant le passage sur suchting. Mais si on va plus loin, on s'aperçoit que Fedor Duz-Khotimirsky finit derrière Suchting dans ce fameux tournoi de Karlsbad 1911. Or 2 ans plus tôt, il bat Lasker et Rubinstein. Cela incite-t-il à penser que l'ensemble des joueurs était décidément plus faible ou que le niveau de jeu de certains joueurs (en particulier en dessous du top) était bien plus variable à l'époque que maintenant ? Et puis, le nombre de gaffe est primordial, mais ne caractérise pas à lui seul le niveau de jeu.
|
|
|
Si je décide de publier les bourdes d'un joueur, je prendrai moi aussi un joueur décédé plutôt qu'Azmaïparachvili. On n'est jamais trop prudent.
|
|
|
Superbe! Ca me rappelle les débats de FE de 2002-2003! Bravo! (et je suis sincére).
|
|
|
@dan31 : C'est intéressant que tu cites Duz-Khotimirsky, car Nunn en parle aussi, et c'est pour en remettre une couche.
"Comment Süchting [qu'était nul] s'est-il débrouillé pour marquer 11.5 points face à une telle opposition ? Alors c'est vrai qu'il a eu de gros coups de chance (Duz-Khotimirsky perdit au temps dans une finale de tours complètement gagnante avec deux pions de plus, Alapine accepta la nulle dans une position où il aurait pu gagner une pièce). Mais dans d'autres parties il aurait pu espérer mieux (face à Levenfish, ou Cohn).
Pour en revenir à la question, la réponse est simple : les autres joueurs ne valaient pas mieux [pan dans les dents]. Si on admet que Süchting valait 2100, alors son score implique que la moyenne du tournoi était à 2129."
|
|
|
Je ne fais que transmettre une partie de l'analyse de Nunn, trouvée par hasard dans un livre d'exercices (il utilise, après, des positions du tournoi).
Et oui, relever les gaffes c'est arbitraire. Mais l'étude a le mérite d'exister, et l'indicateur choisi est simple, clair, quantitatif.
A mon avis, ce n'est pas moins fiable ou légitime qu'une notation cybernétique complète.
De plus, Nunn double ce constat objectif d'une analyse subjective que lui permet son niveau de fort GMI ( il peut reconnaître la faiblesse d'un 2100, alors que moi qui surnage à 1900 j'en serais incapable).
Je reste réservé malgré tout, car certaines erreurs relevées (celle de mon diagramme par exemple) ne prouvent pas un niveau 2100, mais encore bien plus bas (alors quoi ? le top 1911 valait 2000 Elo?).
Et certains joueurs étaient encore un peu tendres : Tartacover, qui s'en prend plein la tête, ou Alekhine, qui reste encore aux yeux de beaucoup l'un des plus grands en valeur absolue.
Je pense que Nunn est sévère également lorsqu'il dit que statistiquement peu de parties de ces années-là valent le détour. Il prétend ainsi que, pour Karlsbad 1911, seules Teichmann-Schlechter et Chajes-Tartacover sont passées à la postérité.
Il oublie au moins Duras-Cohn, repérée par Le Lionnais et remise à l'honneur récemment par Georges Bertola (EE n°595, janvier 2010).
44.Txh7+ (Bertola : "superbe retour de flamme digne d'une étude") Rxh7 45.De7+ Rg6 46.Tg8+ Rf5 47.Txg5 (le Lionnais : "La perfection dans la férocité", Bertola : "Plus précisément, une jolie pointe qui force le gain de la Dame) Rxg5 48.Dg7+ (Tarrasch : "Partie défectueuse sur le plan stratégique, brillante tactiquement")

|
|
|
@ elkine : je ne comprends pas cette remarque. Le but de Nunn était de chercher ce que valaient réellement les meilleurs joueurs du début du XXème siécle. Il dit même qu'il ne savait pas à quel résultat s'attendre, ce qui me surprend fort, car j'imagine les compétiteurs de la Belle-Epoque beaucoup moins entraînés et professionnels que ceux des décennies suivantes.
Par ailleurs, je sais que cet article ne rentre pas dans le cadre initial de ce débat, qui parlait d'une inflation éventuelle du Elo.
Cette contribution est plutôt méthodologique.
On pourrait reprendre un tournoi du début des années 70 et un contemporain pour analyse, avec les caractéristiques énoncées par John Nunn : beaucoup de parties, joueurs de niveaux variés.
Si on avait la même moyenne Elo, en plus, ce serait le pompon.
|
|
|
S'il s'agit de la remarque d'elkine du 17 janvier, il me semble qu'il faisait seulement allusion au risque pour sa vie, Azma étant, tout comme une certaine idole des fouteballeux, réputé pour ses coups de boule.
Pour le reste, infiniment cher Atms, un auteur qui ne retient que deux parties "passées à la postérité" du tournoi de Karlsbad 1911 signe par là même son imposture. Tout lecteur qui ne jette pas, à cet instant, le livre à la poubelle n'aura par la suite que (désolé)... ce qu'il mérite.
|
|
|
Atms : si Reyes m'offre, disons, 3000 euros (je ne suis pas gourmand), je m'engage à revoir attentivement les 325 parties de Karlsbad et à présenter sur FE tout ce qui mérite de "passer à la postérité".
NB : je ne suis pas inquiet, j'ai dans le passé fait le même travail pour Vienne 1903. La moisson était plus qu'abondante !
|
|
|
http://www.youtube.com/watch?v=MwntXN8RXBQ
On évoque Laplace à partir de 19 minutes dans cette vidéo!!
|
|
|
A 16 minutes aussi...et aussi avant,vers 7 minutes on évoque sa biographie...
|
|
|
Je vais essayer d'apporter mes lumières de chercheur sur la question.
Tu as raison d'assumer qu'en absence d'informations il est douteux de parier sur l'équiprobabilité. C'est pour cela qu'on a inventé la "logique possibiliste" qui permet de distinguer les cas d’équiprobabilités des cas où on manque d'informations.
Cependant, lorsque par exemple il est nécessaire d'associer une valeur numérique au résultat (faire un pari par exemple) il faut bien choisir selon des critères numériques et, dans ce cas, supposer une équiprobabilité n'est pas le plus mauvais des choix.
Autre sujet, il a été montré l'an dernier qu'il n'y avait pas d'inflations de Elo mais bel et bien une augmentation du niveau des joueurs. En d'autres termes, Carlsen mettrait probablement une fessée à Fischer. (voir http://www.aaai.org/ocs/index.php/AAAI/AAAI11/paper/view/3779).
La preuve est vraiment convaincante: maintenant que les programmes sont vraiment plus forts que les humains, on peut se servir des suggestions des programmes pour évaluer le niveau de jeu des humains. Et la déviation par rapport aux suggestions de la machine est comparable lorsque les ELO sont comparables quelque soit l'année.
|
|
|
Comme évoqué dans la discussion ce genre de test me semble avoir du sens pour un échantillon significatif de joueurs, par exemple pour des 2250, mais pas des masses complétement à l'extrémité de la répartition.
En gros Carlsen joue essentiellement des joueurs dans la fourchette 2750-2800 et réalise bon an mal an un bon 60 %. Du temps de Fischer, il n'y avait personne dans cette fourchette, enfin mon sentiment est que plus on s'éloigne du centre de la distibution et moins les classements ont de sens.
Pour donner un exemple de ce que je veux dire, au moment où je jouais le mieux il y avait plus de 150 points d'écart entre mon classement FIDE et le classement FFE que j'aurais eu à la même date.
Le classement FFE correspondait pourtant à la perf parce que je jouais beaucoup. Mais en admettant que je garde le même niveau de jeu, la progression au classement aurait modifié le niveau de l'opposition et il n'est pas dit du tout que la performance FFE serait restée constante.
Je pense que non, d'ailleurs, et pourtant mathématiquement elle était plus conforme au mode de calcul du classement que la variation du classement FIDE qui était aussi directement impactée par le nombre de parties disputées.
En d'autres termes, ce n'est pas parce que l'on fait 75 % conrte une moyenne à 2200 que l'on fait 50% contre une moyenne à 2400 et encore moins 25% contre une moyenne à 2600.
Mais tant qu'il y a une population d'une certaine taille et brassée des ajustements se font au fur et à mesure et l'échelle garde une cohérence, par contre dans les hautes altitudes ça ne veut plus dire grand chose.
|
|
|
Quel est le score actuel de Carlsen contre les 2600+,en excluant les 2700+ ainsi que les 2800+?Il faudrait comparer avec RJ Fischer...
On peut aussi remplacer 2600+ par joueur évoluant entre la 250éme et la 50éme place mondiale.
Une autre méthode d'ailleurs me vient en tête d'ailleurs,comme il n'y avait que le classement USCF à l'époque de Fischer,dés 1960,et ensuite très peu de temps le classement FIDE,avec donc pas tant de joueurs que ça,on pourrait comparer les scores de Fischer contre les 2700+ USCF pour se faire une idée,ou même mieux,comparer les scores contre les joueurs dans les 50 meilleurs américains...
EDIT: encore faudrait-il être sûr que le niveau à partir du 50éme américain et par tranches de 10 places,soit comparable...donc moduler les pourcentages selon les classements et aussi selon que ce soient ceux de carlsen ou ceux de Fischer...
Compliqué tout ça.
Et on pourrait faire de même avec Kasparov pour savoir qui est réellement le plus fort...
|
|
|
En espérant que cette auto-promo ne dérange pas reyes, je viens d'écrire un article sur l'irrationalité en matière de paris. Ca rejoint un peu ce qui a pu être dit ici ou dans les autres fils, même si je n'ai pas évoqué les paris où l'on ne connait pas l'espérance...
|
|
|



