|
| Clusters illégaux par EricAngelini1 le
[Aller à la fin] |
| Problèmes | |
Bonsoir à tous,
je me demandais si tous les clusters illégaux ne comportant que deux Rois et n pions avaient été illustrés, pour n allant de 1 à 16 (éventuellement avec solution unique).
Pardonnez mon ignorance si ce problème est connu.
|
|
|
Je ne connais pas ce problème, mais c'est intéressant. On peut même dire qu'il y a 35 problèmes à créer : les couples (m,n) avec m>=n.
Je suppose que tu en as cherché quelques-uns.
Pour tout le monde : un illegal cluster est une position illégale, qui devient légale quelle que soit la pièce enlevée (sauf les rois).
|
|
|
Hello FPC,
je vais en effet proposer bientôt qq diagrammes -- mais que représente ton "m" ? Ce qui est vrai, c'est que le nombre d'enoncés est > 16 dès qu'on exige une couleur de pion dans la question. Ainsi deux Rois + "Ajouter 2 pions pour constituer un IC" n'est pas la même chose que deux Rois + "Ajouter 2 pions noirs pour constituer un IC".
|
|
|
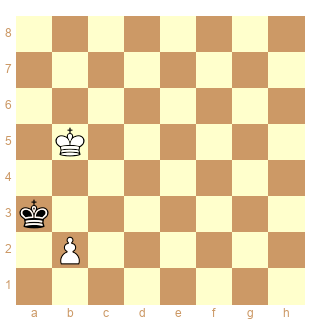
Voici un diagramme pour illustrer la problématique évoquée ("IC" = "Illegal Cluster").
"Ajouter un pion pour former un IC" :

|
|
|
Je crois que la solution (unique) est : pion blanc en b2. La nouvelle position est illégale. Elle devient légale en supprimant ce pion.
|
|
|
Avançons avec le même diagramme (de Rois) mais demandons de former un IC en ajoutant deux pions. Je crois que la solution unique est :

|
|
|
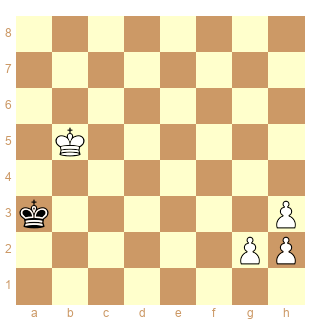
Toujours avec le même diagramme de départ, un IC avec trois pions (à solution non unique) pourrait être :
|
|
|
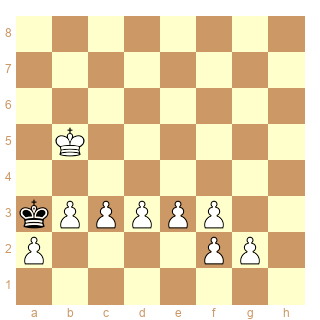
Le principe "de l'escalier" mis en œuvre ci-dessus permet de produire un diagramme répondant à la même contrainte (position des Rois) mais avec 8 pions :
|
|
|
Vous avez compris l'idée. La condition "IC avec deux Rois + n pions" est donc simple à illustrer pour n allant de 1 à 8. Pour le reste (et d'autres conditions sur les couleurs des pions), je ne sais pas...
|
|
|
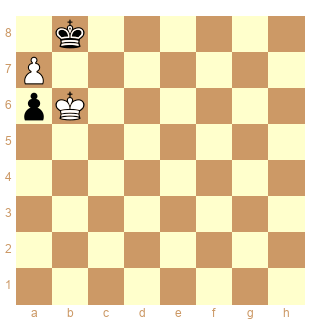
Les entiers m et n représentent les nombres de pions blancs et noirs, en prenant la convention que le nombre de pions blancs est supérieur ou égal au nombre de pions noirs.
Il y a donc (1,0) (2e diagramme), (1,1), (2,0) (3e diagramme), (2,1), (2,2), (3,0) (4e diagramme),… , (8,0) (5e diagramme),…(8,8). Si je ne me trompe pas, ça fait donc 35.
|
|
|
Par exemple pour le (1,1) :
|
|
|
Bien vu, FPC, bon système de notation, merci !
|
|
|
Bon, voilà, on n'est jamais aussi bien servi que par ses propres nuits !
"Ajouter 16 pions au diagramme ci-dessous pour former un IC".

|
|
|
Voici une solution possible (il y a peut-être moyen de ne produire qu'une solution unique en disposant les Rois autrement) :

|
|
|
La position ci-dessus est illégale : les pions blancs ont effectués 7 prises, or ceci est impossible car le Fou noir en c8 n'a pu bouger (seules les 2 tours noires, les 2 cavaliers noirs, le fou f8 et la dame d8 ont pu se sacrifier sur la 3e rangée -- ce qui fait 6 pièces).
Dès qu'on ôte un pion blanc, la position devient légale (ôter a2 ou a3 permet qu'il n'y ait eu aucune capture dans le passé ; ôter b3 n'exige plus qu'une capture, ôter c3 deux captures, ôter d3 trois captures... jusqu'à ôter g3 qui exigera 6 captures -- précisément celles mentionnées plus haut).
Ne pas toucher aux pions blancs et ôter l'un quelconque des pions noirs rend aussi la position légale : en envoyant ce pion à promotion on obtiendra les 7 captures nécessaires justifiant l'actuelle 3e rangée : les 6 pièces noires mentionnées plus haut et celle issue de promotion.
J'espère que je ne me suis pas planté... au cours de la nuit !
(on notera que les Rois ne jouent aucun rôle ici.)
|
|
|
Note pour FPC : on peut se passer de la condition m>=n si on convient que le premier chiffre indique la quantité de pions blancs et le second la quantité de pions noirs. Ainsi demanderait-on ci-avant : "IC (8,8)". Voici une solution où les promotions n'interviennent plus (je ne détaille pas la solution, les mêmes principes s'appliquent) :

|
|
|
Bonsoir,
Un ami m'a aidé à ouvrir les yeux :
1. Nc3 e6 2. Nb5 Ba3 3. bxa3 Nc6 4. Bb2 Qh4 5. Bf6 gxf6 6. Nf3 Nd4 7. Nxh4 Nb3 8. cxb3 Ke7 9. Qc2 b6 10. Kd1 Ba6 11. Kc1 Bxb5 12. Kb2 Nh6 13. Rg1 Rhg8 14.Ng6+ Rxg6 15. Qf5 Nxf5 16. Rc1 Rg3 17. Rc4 Rh3 18. gxh3 Rg8 19. Rg3 Rxg3 20.fxg3 Kd6 21. Bg2 Bxc4 22. Be4 Ne3 23. Bg6 fxg6 24. Ka1 Bd5 25. Kb2 Bf3 26. exf3 Kd5 27. Ka1 Kd4 28. Kb2 Kd3 29. Ka1 Nd5 30. Kb2 Ke2 31. Ka1 Nc3 32. dxc3 Kf2 33. Kb2 Kg2 34. Ka1 Kh1 35. Kb2 a6 36. Ka1 c6 37. Kb2 d6 38. Ka1 h6 et le dernier diagramme est atteint...
Merci Lapin !
Quiquine
|
|
|
Bon sang mais c'est bien sûr !
Bien vu Lapin !
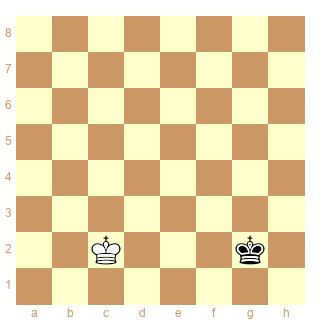
Je vais me venger avec le diagramme ci-dessous et bien vous pourrir la nuit, j'espère (malheureusement les 5 questions ne sont pas trop difficiles, j'en ai peur) ! Il s'agit à chaque fois de fabriquer un nouvel IC en repartant du diagramme du bas et en lui ajoutant :
a) 2 pions B et 2 pions N
b) 2 tours B et 2 tours N
c) 2 cavaliers B et 2 cavaliers N
d) 2 fous B et 2 fous N
e) 2 dames B et 2 dames N.
Aucune des solutions n'est unique...
Bonne nuit (et encore bravo pour la démolition !-)
|
|
|
Une autre présentation de mon 10/07 de 13:49.
Position illégale ci-dessous car B a fait 4 prises avec ses pions au minimum et la structure des pions N n'en permet que 3 : la dame N et ses 2 cavaliers.
Dès qu'on ôte un pion B, 3 prises suffisent pour justifier la nouvelle position blanche, qui devient donc légale (comme l'ensemble du diagramme).
Dès qu'on ôte un pion N, les 3 pièces N mentionnées et le pion ôté (qui se sera promu) constitueront les 4 pièces N qui se sacrifieront pour rendre la nouvelle position légale à son tour.

|
|
|
Bon, ça tourne au monologue -- encore ceci puis je me tais !
L'astuce de Lapin et Alekhikin m'a permis de composer cet IC où 17 pièces ont été ajoutées sur un échiquier occupé par deux rois. La position est illégale et redevient légale quand on ôte l'une quelconque des 17 pièces. Voyez-vous pourquoi ?
Je réponds en privé ici, le cas échéant (avec l'espoir de ne pas m'être planté) : eric point angelini chez skynet point be.

|
|
|
(Last) Breaking News: je viens de poster ce message sur la liste Retro d'Otto Janko :
> Hello Otto and retro-fans,
I've searched on the Internet but
could not find a chess maximum-record
that deals with the retro-genre.
It's about Illegal Clusters.
What is the maximum number of
pieces that could be added to a
given position to build an IC?
My personal best is 20 but I'm
sure the actual record beats that:
-- if you start with an empty board
and the two Kings on their initial
squares, I guess you can add 20 pieces
to build this position:

|
|
|
Aaaaarrghh, non, il fallait avancer les deux pions noirs d'une case et les placer sur d5 et e5 !
La position illégale ci-dessus ne devient pas légale si l'on retire la Tour a8 ! J'arrête les IC, ça ne me vaut rien !
|
|
|
Et elle ne devient pas légale non plus si l'on retire le Fou c8 ! Il faut qu'il puisse être capturé sur une case blanche ! Le nouveau diagramme (correct ?) aura l'aspect ci-dessous (pardon à tous pour ces lectures très pénibles :-((

|
|
|



