|
| Buts conjugués pour les Nuls par ni***as***o*1240 le
[Aller à la fin] |
| Problèmes | |
Ce fil fait écho à celui que Jean-Christian vient d’ouvrir, en se voulant complémentaire. Autant notre ami se place dans un contexte bien précis et déjà élaboré, autant ici nous allons partir de zéro ou presque, pour peu à peu construire et illustrer la théorie des buts conjugués.
L’idée de base est extrêmement simple : dans la plupart des problèmes d’échecs on demande au dernier coup de la solution (le coup terminal) d’atteindre un but fixé, ici nous demandons que ce coup terminal ne soit plus constitué d’un seul mouvement, mais d’un ensemble de mouvements distincts, chacun réalisant un but d’une liste fixée.
En particulier, à chaque genre ou presque de problèmes d’échecs, va correspondre son alter-ego à buts conjugués. Jean-Christian a donc inventé une sorte d’univers parallèle qu’il nous faut maintenant explorer !
Commençons par le Direct de Série qui, nous allons le voir, pose déjà des difficultés pour être correctement défini et stipulé. Dans ce genre les Blancs jouent tous les coups, pour finalement pouvoir atteindre leur but, mais sans y être obligé. Nous passons dans la dimension supérieure en demandant que les Blancs réussissent à la fois, par deux coups terminaux différents, à capturer une unité noire et à mettre les Noirs en échec, toujours sans y être obligé. Le symbole utilisé pour un tel énoncé est ser-(dx&d+)N, qui signifie capture directe et échec direct en N coups.
Schéma 1 :

ser-(dx&d+)3
On utilise le logiciel Popeye pour la vérification, extrêmement performant et qui semble supporter les buts conjugués, du moins dans certains cas. Le bon candidat pour la s-stipulation associée semble être ici :
sstip white 2s[-1s[+] & -1s[x] & !-1s[+&x]]
Si l’on entre les commandes suivantes (n’oubliez pas votre protocole pour recevoir le résultat dans l’output) :
begin
pieces white Kc4 Pg4h6 black Kg8 Pa7f7
sstip white 2s[-1s[+] & -1s[x] & !-1s[+&x]]
end
On obtient le résultat suivant :
1.Kc4-b5 2.Kb5-a6 3.h6-h7 +
1.Kc4-b5 2.Kb5-a6 3.Ka6*a7 x
Est-ce vraiment ce que l’on souhaite ? Certes la série 1.g5 2.g6 3.gxf7 + n’est pas une solution proposée par le logiciel, et c’est logique puisque c’est la même pièce qui à la fois capture et donne échec, possibilité enlevée par la commande !-1s[+&x]. Mais quid de la possibilité :
1.g5 2.g6 3.h7 +
1.g5 2.g6 3.gxf7
C’est-à-dire lorsque gxf7 est considéré seulement comme un coup capturant. Ou bien on considère que ce n’est pas une solution valide, auquel cas l’énoncé du problème devient « à chaque but est associé un unique coup spécifique, i.e. réalisant uniquement ce but et différent pour chaque but ». Ou bien on considère que c’est une solution valide, auquel cas il faut trouver une autre s-stipulation qui inclus ce style de solution…
Et il y a même pire comme cas de conscience ! Examinons en effet le même problème avec le Pg4 en g6.
Schéma 2 :

ser-(dx&d+)3
Ici Popeye ne donne aucune solution, même pas
1.Kc4-b5 2.Kb5-a6 3.h6-h7 +
1.Kc4-b5 2.Kb5-a6 3.Ka6*a7 x
Il me semble que son “raisonnement” est de dire qu’après 2.Ra6, il reste la possibilité 3.gxf7+ dont il ne veut absolument pas… D’ailleurs si on liste les solutions cette fois en 4 coups, Popeye donne :
1.g6-g7 2.Kc4-b5 3.Kb5-a6 4.h6-h7 +
1.g6-g7 2.Kc4-b5 3.Kb5-a6 4.Ka6*a7 x
1.Kc4-b5 2.g6-g7 3.Kb5-a6 4.h6-h7 +
1.Kc4-b5 2.g6-g7 3.Kb5-a6 4.Ka6*a7 x
1.Kc4-b5 2.Kb5-a6 3.g6-g7 4.h6-h7 +
1.Kc4-b5 2.Kb5-a6 3.g6-g7 4.Ka6*a7 x
C’est-à-dire qu’il évacue systématiquement la possibilité 4.gxf7+ Là encore il y a un choix à faire : ou bien on considère qu’une solution doit être parfaitement « pure » pour être valide (non parasitée par un autre coup pouvant atteindre les 2 buts en même temps), ou bien il faut trouver une autre s-stipulation…
Donc comme on le voit sur ces schémas élémentaires, il y a déjà du boulot pour simplement obtenir des définitions précises de ce que l’on veut, et trouver les s-stipulations adaptées. Si vous le voulez bien, ce sera l’objectif de cette guirlande !
|
|
|
dans cet esprit, nous pouvons imaginer une série à "Buts conjugués terminaux"!
considérons par exemple le problème suivant de jean Christian

si nous changeons le challenge de la position, pour atteindre "soit mat, soit pat" cela revient à:
" trouver la série au terme de laquelle tous les coups terminent la partie "
appelons T ce but et !Tz le zugzwang qui s'y rapporte.
(!Tzn : les blancs jouent n coups de série qui les crontraigent à mettre un Terme à la partie )
le problème ci-dessus admet une solution en quatre coups:
ser-!Tz4 que l'on teste avec la stipulation suivante :
sstip white 4s[-1s[#] & -1s[=] & !-1s[!#&!=]]
nous obtenons un jumeau du problème de référence avec cette particularité qu'ici le coup terminal se doit de "stopper la série & la partie" )
Pieces
White Pf6 Pb5 Pe5 Pd4 Pg4 Pb3
Black Pf7 Ke6 Pd5 Pg5 Pb4
sstip white 4s[-1s[#] & -1s[=] & !-1s[!#&!=]]
EndProblem
la solution est :
1.b5-b6 2.b6-b7 3.b7-b8=S 4.Sb8-d7! !Tz4 (Sd7-c5 #, Sd7-f8 #, Sd7-b6 =, Sd7-b8 =)
tous les coups font Mat ou Pat... et donc après 4.Sb8-d7! !Tz4 les blancs sont contraints de finir la partie.
|
|
|
Certes, mais ça ne répond pas à ma question de savoir quelle sstip utiliser dans le schéma 2. Dans ton cas Dominique le mat et le pat ne peuvent pas être administrés par le même mouvement, donc il n'y a pas d'ennui de sstip.
Mais si par exemple les buts sont l'échec et le mat, tout coup donnant mat donnera à fortiori échec, et donc Popeye ne permettra jamais un mat dans sstip white 2s[-1s[+] & -1s[#] & !-1s[+&#]].
En effet le !-1s[+&#] empêche les coups donnant à la fois échec et mat, donc en fait les coups donnant mat...
|
|
|
concernant le mat sans autre échecs voici une position intéressante .
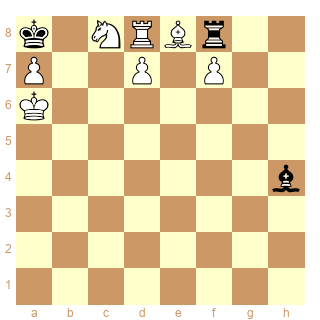
trouver une stipp pour::
échec sans mat
échec et mat pur ( pas d'autre échecs )
échec ou mat
...........................
faire mat et non echec !
...........................
sstip white 1s[(-1s[+] & !-1s[!#]) | (-1s[#] )]
1.Ka6-b6 2.Sc8-e7 #
...........................
faire echec et non mat !
...........................
sstip white 1s[(-1s[+] & !-1s[#]) ]
1.Ka6-a5 2.Sc8-b6 +
1.Ka6-a5 2.Sc8-d6 +
1.Ka6-a5 2.Sc8-e7 +
1.Ka6-b5 2.Sc8-b6 +
1.Ka6-b5 2.Sc8-d6 +
1.Ka6-b5 2.Sc8-e7 +
...........................
faire mat ou echec !
...........................
sstip white 1s[-1s[+] & -1s[#]]
1.Ka6-b6 2.Sc8-d6 +
1.Ka6-b6 2.Sc8-e7 +
1.Ka6-b6 2.Sc8-e7 #
|
|
|
autre version pour cette même sstip en libérant b6 (faire mat et non echec !)
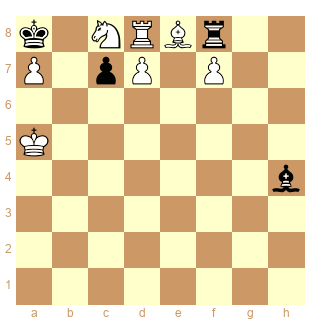
Pieces
White Sc8 Rd8 Be8 Pa7 Pd7 Pf7 Ka5
Black Ka8 Rf8 Pc7 Bh4
sstip white 1s[(-1s[+] & !-1s[!#]) | (-1s[#] )]
1.Ka5-a6 2.Sc8-b6 #
1.Ka5-a6 2.Sc8-e7 #
|
|
|
Tu veux dire que, pour Popeye, un mat à la découverte n'est pas aussi un échec ? Dans ce cas, quelle est la bonne sstip pour le schéma suivant ?
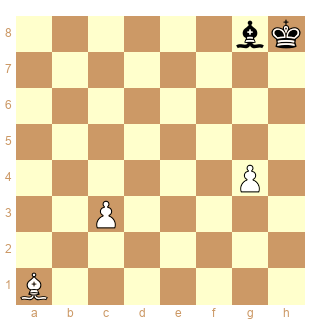
ser-(d+&d#)3
1.g5 2.g6 3.g7+ c4#
|
|
|
Et quid de 2 fois le même but ?
Schéma 4 (celui au-dessus est le schéma 3)
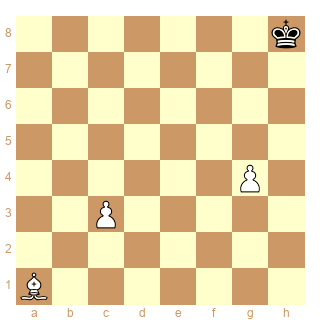
ser-(d+&d+)3
Qui trouvera la bonne sstip qui donne la solution :
1.g5 2.g6 3.g7+ c4+
|
|
|
je veux dire que :
sstip white 1s[(-1s[+] & !-1s[!#]) | (-1s[#] )]
marche très bien ici pour distiguer un échec avec mat d'un echec sans mat le mat primant l'échecs dans cette sstip
3.c4 est bien sûr un échec à la découverte mais l'idée est ici de ne garder que ce qui fait mat:
3.c4 # est conservé parcequ'il fait mat
3.g7+ ne faisant pas mat est ignoré.
1.g5 2.g6 3.c4 # ( seule solution)
mais pour ton ser-(d+&d#)ta propre sstip marche très bien.
sstip white 1s[-1s[+] & -1s[#]]
1.g4-g5 2.g5-g6 3.g6-g7 +
1.g4-g5 2.g5-g6 3.c3-c4 +
1.g4-g5 2.g5-g6 3.c3-c4 #
effectivement elle donne pour chaque solution avec mat une solution redondante avec échec... Il faudrait savoir si Popeye accepte d'effectuer des soustraction de solution :o) mais je ne vois pas comment
|
|
|
pour ton Schéma 4 il n'y a pas de solution ( car le fou garde un tempo )
mais si tu places le pion c en b2 (au prix d'une illégalité :o( de position mais bon! nous sommes en atelier ) alors
ça marche en ser-(d+&d+)3 avec 2s[-1s[+] & !-1s[!+]]
Pieces
White Pg4 Pb2 Ba1
Black Bg8 Kh8
sstip white 2s[-1s[+] & !-1s[!+]]
1.g4-g5 2.g5-g6 3.g6-g7 +
1.g4-g5 2.g5-g6 3.b2-b4 +
1.g4-g5 2.g5-g6 3.b2-b3 +
ser-(d+&d+)3
et cela semble accepté également pour le mat !
Pieces
White Pg4 Pb2 Ba1
Black Bg8 Kh8
sstip white 1s[(-1s[+] & !-1s[!#]) | (-1s[#] )]
1.g4-g5 2.g5-g6 3.b2-b4 #
1.g4-g5 2.g5-g6 3.b2-b3 #
ser-(d#&d#)3
|
|
|
Ca c'est le cas du double mat forcé. Donc c'est du ser-!(#z&#z)2 ou quelque chose de cet acabit.
C'est très intéressant, mais je me place dans le cas des séries directes classiques (pas d'obligation d'atteindre les buts, seulement la possibilité). En particulier j'ai fait exprès de laisser un mouvement libre au Fou.
Paradoxalement les bonnes sstip semblent plus délicates à trouver dans ce cadre, par exemple pour le schéma 3, pourtant élémentaire.
|
|
|
Bravo pour le cas du double échec obligatoire, ça marche du feu de Dieu !

ser-!(+z&+z)3 C+
white 3s[-1s[+] & !-1s[!+]]
1.a2-a4 2.a4-a5 3.a5-a6 (4.g6-g7 + b2-b3 +)
|
|
|
Le double mat obligatoire aussi !

ser-!(#z&#z)6 C+
white 6s[-1s[#] & !-1s[!#]]
1.Kd1-e2 2.Ke2-f3 3.Kf3-g4 4.Kg4-h5 5.Kh5-h6 6.h4-h5 (7.g6-g7 # b2-b3 #)
Il reste à trouver la bonne sstip pour le double but identique dans le cadre facultatif...
|
|
|
pour le cas de l'aidé voici une illustration qui peut nous aider à trouver la bonne sstip pour le double but identique dans le cadre facultatif:

mat aidé en deux coups de série :
1.c3-c4 2.Kb2*b3 #
echec seul aidé en un coups de série :
1.g6-g7 +
les sstips suivantes semblent marcher .
----------------------------------------------
mat seul aidé en n : ns[#] | !ns[!#]
Pieces
White Pg6 Pg5 Ph4 Pc3 Kb2 Ba1
Black Bg8 Kh8 Pb4 Pb3
sstip white 3s[#] | !3s[!#]
Option Variation NoBoard
EndProblem
1.c3-c4 2.Kb2*b3 #
1.h4-h5 2.c3-c4 3.Kb2*b3 #
1.c3-c4 2.h4-h5 3.Kb2*b3 #
1.Kb2-b1 2.Ba1-b2 3.c3*b4 #
1.Kb2-b1 2.Ba1-b2 3.c3-c4 #
1.Kb2-c1 2.Ba1-b2 3.c3*b4 #
1.Kb2-c1 2.Ba1-b2 3.c3-c4 #
----------------------------------------------
echecs seul aidé en n : ns[+] | !ns[!+]
Pieces
White Pg6 Pg5 Ph4 Pc3 Kb2 Ba1
Black Bg8 Kh8 Pb4 Pb3
sstip white 2s[+] | !2s[!+]
Option Variation NoBoard
EndProblem
1.g6-g7 +
1.h4-h5 2.g6-g7 +
1.c3-c4 2.g6-g7 +
1.c3-c4 2.Kb2-c1 +
1.c3-c4 2.Kb2-b1 +
1.c3-c4 2.Kb2*b3 +
1.c3*b4 2.g6-g7 +
1.c3*b4 2.Kb2-c1 +
1.c3*b4 2.Kb2-a3 +
1.c3*b4 2.Kb2-b1 +
1.Kb2-b1 2.g6-g7 +
1.Kb2-b1 2.c3*b4 +
1.Kb2-b1 2.c3-c4 +
1.Kb2-c1 2.g6-g7 +
1.Kb2-c1 2.c3*b4 +
1.Kb2-c1 2.c3-c4 +
|
|
|
non c'est trivial : il ne s'agit que de
mat seul aidé en n : ns[#]
echec aidé en n : ns[+]
ça ne marche pas ! désolé.
|
|
|
essai de correction :
schéma 5: echecs aidés en n coups sans mat
ns[-1s[+] & !-1s[#]]

Pieces
White Pg6 Pg5 Ph4 Pc3 Kb2 Ba1
Black Bg8 Kh8 Pb4 Pb3
sstip white 1s[-1s[+] & !-1s[#]]
Option Variation NoBoard
EndProblem
1.h4-h5 2.g6-g7 +
1.c3*b4 2.g6-g7 +
1.c3*b4 2.Kb2-c1 +
1.c3*b4 2.Kb2-a3 +
1.c3*b4 2.Kb2-b1 +
1.Kb2-b1 2.g6-g7 +
1.Kb2-b1 2.c3*b4 +
1.Kb2-b1 2.c3-c4 +
1.Kb2-c1 2.g6-g7 +
1.Kb2-c1 2.c3*b4 +
1.Kb2-c1 2.c3-c4 +
notons l'évitement de
1.Kb2*b3? 2.c3*b4 + & #
1.Kb2*b3? 2.c3-c4 + & #
|
|
|
notons l'évitement de
1.c3-c4 ? 2.Kb2*b3 + & #
et non 1.Kb2*b3?? qui est un auto échec ! :o(
je fatigue !
|
|
|
Afin de cerner au mieux la difficulté, autant travailler sur une matrice extrêmement dépouillée, sans échec ni mat, par exemple :
Schéma 6
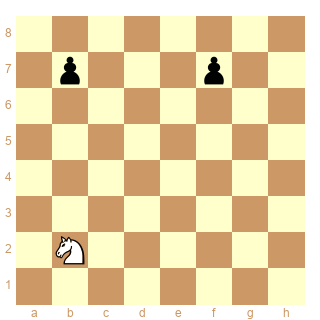
ser-(dx&dx)3
La bonne sstip doit donner la solution :
1.Cc4 2.Cd6 3.Cxb7 x
1.Cc4 2.Cd6 3.Cxf7 x
Je ne la trouve pas et ça m'énerve...
|
|
|
Arggg erreur ! Le schéma 6 pose une question différente, la double capture par une même unité. Ce qu'on veut c'est que 2 unités puissent capturer au même moment, par exemple :
Schéma 7
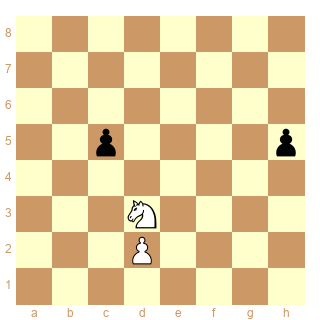
ser-(dx&dx)3
La bonne sstip doit donner la solution :
1.Cf4 2.d4 3.dxc5 x
1.Cf4 2.d4 3.Cxh5 x
|
|
|
oui, pour le diagramme précédent j'avais
Pieces
White Sb2
Black Pb7 Pf7
sstip white 2s[(-1s[x] & !-1s[!x]) |-1s[x]]
1.Sb2-d3 2.Sd3-e5 3.Se5*f7 x
1.Sb2-d3 2.Sd3-c5 3.Sc5*b7 x
1.Sb2-c4 2.Sc4-e5 3.Se5*f7 x
1.Sb2-c4 2.Sc4-d6 3.Sd6*f7 x
1.Sb2-c4 2.Sc4-d6 3.Sd6*b7 x
1.Sb2-c4 2.Sc4-a5 3.Sa5*b7 x
1.Sb2-a4 2.Sa4-c5 3.Sc5*b7 x
mais il me parait impossible d'isoler la variante 1.Sb2-c4 2.Sc4-d6 ( Sd6*b7x, Sd6*f7x)
|
|
|
Oui je commence aussi à penser que c'est impossible, aussi bien pour le schéma 6 que le schéma 7. Si les buts A et B sont distincts, on peut enlever les solutions qui ne permettent que A et les solutions qui ne permettent que B. Il ne reste alors que ce qu'on veut, les solutions qui permettent A et B. Mais si A=B cette astuce ne marche pas...
Ca marche si A=B dans le cadre du but obligatoire parce qu'on enlève toute possibilité de solution à part celles qui permettent A.
|
|
|
dans ce cas précis on peut y arriver ...mais en "trichant" sur le but (z et non x )
Pieces
White Sd3 Pd2
Black Pc5 Ph5
sstip white 2s[-1s[Zc5] & -1s[Zh5]]
Option Variation NoBoard
EndProblem
1.Sd3-f4 2.d2-d4 3.d4*c5 z
1.Sd3-f4 2.d2-d4 3.Sf4*h5 z
comme nous sommes dans le cadre d'un direct de série... les pièces noires ne bougeant pas, cela reste une possibilité, inélégante mais apparemment(?) correcte.
l'idée est qu'une pièce blanche ne peut occuper la place d'une pièce noire sans la capturer (!)
o, peut en conclure -(indirectement) le C+de ton schéma 7:
1.Sd3-f4 2.d2-d4 (dx&dx) (d4*c5x, Sf4*h5x)
|
|
|
étrangement cela marche aussi dans le schéma 6:
Pieces
White Sb2
Black Pb7 Pf7
sstip white 2s[-1s[Zb7] & -1s[Zf7]]
1.Sb2-c4 2.Sc4-d6 3.Sd6*b7 z
1.Sb2-c4 2.Sc4-d6 3.Sd6*f7 z
|
|
|
C'est assez logique que ça marche puisque tu remplaces 2 buts identiques par 2 buts différents ! Mais on ne peut hélas pas toujours utiliser une telle astuce. Par exemple dans le schéma 4 on ne peut pas remplacer ++ par 2 buts distincts.
|
|
|
enfin pour le schéma 2, nous pouvons révéler la solution(duale par interversion de coups . Mais ici il faut avoir idée de la solution pour déterminer les cases est Zugzwang... ce qui est trivial ici mais rédhibitoire dans l'absolu.
Pieces
White Pg6 Ph6 Kc4
Black Kg8 Pa7 Pf7
sstip white 2s[ -1s[x] & !-1s[+&x] & (-1s[Za7]& -1s[Zh7])]
1.g6-g7 2.Kc4-b5 3.Kb5-a6 4.Ka6*a7 x
1.g6-g7 2.Kc4-b5 3.Kb5-a6 4.Ka6*a7 z
1.g6-g7 2.Kc4-b5 3.Kb5-a6 4.h6-h7 + z
1.Kc4-b5 2.g6-g7 3.Kb5-a6 4.Ka6*a7 x
1.Kc4-b5 2.g6-g7 3.Kb5-a6 4.Ka6*a7 z
1.Kc4-b5 2.g6-g7 3.Kb5-a6 4.h6-h7 + z
1.Kc4-b5 2.Kb5-a6 3.g6-g7 4.Ka6*a7 x
1.Kc4-b5 2.Kb5-a6 3.g6-g7 4.Ka6*a7 z
1.Kc4-b5 2.Kb5-a6 3.g6-g7 4.h6-h7 + z
cette méthose sera très artificielle dans le cadre de but conjugués autre que la prise.
croisement: oui! c'est très limité!
|
|
|
dans le cas particulier du schéma4 , c'est possible mais c'est une originalité liée à la position.
Pieces
White Pg4 Pc3 Ba1
Black Kh8
sstip white 2s[-1s[+] & (-1s[Zc4] & -1s[Zg7]) ]
1.g4-g5 2.g5-g6 3.g6-g7 +
1.g4-g5 2.g5-g6 3.c3-c4 +
1.g4-g5 2.g5-g6 3.c3-c4 + z
1.g4-g5 2.g5-g6 3.g6-g7 + z
|
|
|
Oui mais tu n'as pas prouvé le C+ puisqu'il pourrait exister d'autres solutions sur d'autres cases que celles que tu as spécifié...
|
|
|
Donc si on se résume, le cas des buts obligatoires est réglé, et dans le cas des buts facultatifs il reste à trouver la bonne sstip pour A=B et pour les coups qui réalisent A&B.
Dans ce dernier cas, voici une matrice sans échec ni mat, qui cerne bien la difficulté :
Schéma 8

ser-(dx&df6)3
La solution
1.g4 2.g5 3.gxf6 z
1.g4 2.g5 3.bxa3 x
n'est pas détectée par Popeye avec la sstip white 2s[-1s[zf6] & -1s[x] & !-1s[zf6&x]]. La raison est qu'il refuse gxf6 qui atteint la bonne case, mais en capturant. Pourtant nous avons besoin de cette solution sinon jamais rien ne marchera avec # et + comme buts, puisque Popeye refusera toujours de donner mat, un tel coup étant aussi un échec.
Il faut passer à 5 coups et la sstip white 4s[-1s[zf6] & -1s[x] & !-1s[zf6&x]] pour que Popeye donne :
1.g2-g4 2.g4-g5 3.g5*f6 4.f6-f7 5.f5-f6 z
1.g2-g4 2.g4-g5 3.g5*f6 4.f6-f7 5.b2*a3 x
Ici la case f6 est atteinte par un coup non capturant, donc c'est valide pour Popeye.
|
|
|
voici quelque chose de satisfaisant .
A = ensemble des coups atteignant le premier but .
B = ensemble des coups atteignant le second but .
C = ensemble des coups n'atteignant pas l'un des buts .
solution = A & B | !C
Pieces
White Pf5 Pb2 Pg2
Black Pf6 Pa3
sstip white 2s[-1s[zf6] & -1s[x] | !-1s[!zf6|!x]]
1.g2-g4 2.g4-g5 3.g5*f6 z
1.g2-g4 2.g4-g5 3.g5*f6 x
1.g2-g4 2.g4-g5 3.b2*a3 x
que l'on peut écrire:
1.g2-g4 2.g4-g5 3.g5*f6 zx
1.g2-g4 2.g4-g5 3.b2*a3 x
|
|
|
oops je n'arrive pas à coller l'idée au schéma 2 ... je m'y replonge !
|
|
|
Ah super, bravo on avance ! Ta technique marche aussi pour le schéma 1, avec la sstip white 2s[-1s[x] & -1s[+] | !-1s[!x|!+]], Popeye donne (enfin !) le résultat attendu :
1.g4-g5 2.g5-g6 3.g6*f7 + x
1.g4-g5 2.g5-g6 3.h6-h7 +
1.g4-g5 2.g5-g6 3.g6*f7 +
1.Kc4-b5 2.Kb5-a6 3.Ka6*a7 x
1.Kc4-b5 2.Kb5-a6 3.h6-h7 +
Il suffit alors de présenter ces 2 solutions sous la forme :
1.g4-g5 2.g5-g6 3.g6*f7 x
1.g4-g5 2.g5-g6 3.h6-h7 +
1.Kc4-b5 2.Kb5-a6 3.Ka6*a7 x
1.Kc4-b5 2.Kb5-a6 3.h6-h7 +
Croisement : si si ça fonctionne aussi au schéma 1, il y a plein de solutions, toutes détectées par Popeye, et même en 1 coup avec 1.g6*f7 + x, mais que Popeye ne donne pas car il lui faut au moins un coup de série avant de réaliser le but.
|
|
|
oui mais je dois faire une erreur de raisonnement pour le schéma 2
Pieces
White Pg6 Ph6 Kc4
Black Kg8 Pa7 Pf7
sstip white 2s[-1s[x] & -1s[Za7] & -1s[Zh7] | (!-1s[+&x] |!-1s[Za7] |!-1s[Zh7])]
1.Kc4-b5 2.Kb5-a6 3.g6*f7 + x
1.Kc4-b5 2.Kb5-a6 3.Ka6*a7 x
1.Kc4-b5 2.Kb5-a6 3.Ka6*a7 z
1.Kc4-b5 2.Kb5-a6 3.h6-h7 + z
que l'on peut écrire:
1.Kc4-b5 2.Kb5-a6 3.g6*f7 + x (??)
1.Kc4-b5 2.Kb5-a6 3.Ka6*a7 zx
1.Kc4-b5 2.Kb5-a6 3.h6-h7 + z
pourquoi la première solution persiste t-elle?
je sais bien sûr que je fais une erreur mais je pense manquer de lucidité... si tu trouve le bug c'est bon!
|
|
|
C'est nickel aussi au schéma 3 !
white 2s[-1s[#] & -1s[+] | !-1s[!#|!+]]
1.g4-g5 2.g5-g6 3.c3-c4 #
1.g4-g5 2.g5-g6 3.g6-g7 +
1.g4-g5 2.g5-g6 3.c3-c4 +
Tu es le grand chaman de la sstip, Dominique !
Croisement: la même sstip white 2s[-1s[x] & -1s[+] | !-1s[!x|!+]] fonctionne au schéma 2 (plein de solutions, c'est normal).
|
|
|
Bah! un humble padawan Maître Nicolas !
|
|
|
mais j'y pense :
peut être que la solution attendue au schéma 2 est effectivement :
1.Kc4-b5 2.Kb5-a6 3.g6*f7 + x
1.Kc4-b5 2.Kb5-a6 3.Ka6*a7 zx
1.Kc4-b5 2.Kb5-a6 3.h6-h7 + z
car " g6*f7 +x " atteint bien le but! il atteint deux des buts en fait et cela peut ( doit?) être considéré comme correct ) à moins que tu ne cherche un "ou exclusif" ça marche nickel
|
|
|
Avoue, tu as trouvé cette sstip en examinant les entrailles d'un poulet !
|
|
|
sans doute quelque merveilleux cours de logique en septembre 1976 à l'université Catholique de l'Ouest d'Angers... je m'en souviens avec ravissement! ^^
|
|
|
Pour moi le schéma 2 est un (dx&d+)1, avec comme solution 3.g6*f7 + x. Mais on ne peut pas le vérifier en série, il va falloir maintenant trouver les sstip dans les énoncés avec alternance des coups...
|
|
|
sstip white 2s[-1s[x] & -1s[+] | !-1s[!x|!+]] marche effectivement mais
sstip white 2s[-1s[x] & -1s[Za7] & -1s[Zh7] | (!-1s[+&x] |!-1s[Za7] |!-1s[Zh7])]
fait un gros ménage dans les répétitions ! ^^ ( au prix de l'utilisation du Zug en guise de GPS.
je suis assez content sur ce coups là !
|
|
|
Si on commmence par l'aidé en n coups, on peut espérer que la bonne sstip soit :
sstip black (2n-1)h[comme en série]h
|
|
|
Ca à l'air de fonctionner nickel grâce à la sstip magique !
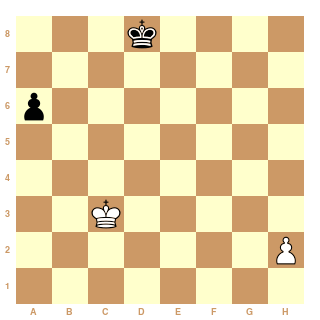
(hx&h+)3
black 5h[1s[x] & 1s[+] | !1s[!x|!+]]h
1.Kd8-e7 Kc3-b4 2.Ke7-f6 Kb4-a5 3.Kf6-g5 Ka5*a6 x
1.Kd8-e7 Kc3-b4 2.Ke7-f6 Kb4-a5 3.Kf6-g5 h2-h4 +
|
|
|
avant de passer aux aidés voici un petit problème qui m'a guidé dans la recherche de la sstip( avec des coups libres de pions qui m'otaient toute solution... mais ça c'était avant.) et que j'ai pu corriger/allèger grace à cette dernière

ser-(dx&d+)3
2 solutions C+
Pieces
White Pc6 Ph6 Pg5 Pe4 Kd3 Pe3
Black Sd8 Kg8 Pa7 Pc7 Pe6 Rh5
sstip white 3s[-1s[x] & -1s[+] | !-1s[!x|!+]]
1.Kd3-c4 2.Kc4-b5 3.Kb5-a6 4.Ka6*a7 x
1.Kd3-c4 2.Kc4-b5 3.Kb5-a6 4.h6-h7 +
1.Kd3-e2 2.Ke2-f3 3.Kf3-g4 4.Kg4*h5 x
1.Kd3-e2 2.Ke2-f3 3.Kf3-g4 4.h6-h7 +
croisement: ton petit problème didactique semble démonter que tout baigne ! je n'aurais jamais parié que l'affaire serait aussi avancée en moins de 24 heures. ( le cachet de FE faisant foi! )
|
|
|
Ce qui est vraiment extraordinaire avec cette sstip est qu'elle fonctionne toujours, qu'il y ait conflit ou pas entre les 2 buts. De plus en changeant seulement 2 signes (&& à la place de ||), on passe facilement de but facultatif à but obligatoire. Vraiment une belle découverte !
Si ça t'intéresse Dominique, tu as largement gagné le droit d'être co-auteur de l'article à venir sur les buts conjugués, je suis certain que JC partage cet avis.
Il va pas falloir se rater, prendre son temps, trouver des inédits puissants (en demandant l'aide de collègues ?), on tient un sujet en or massif...
|
|
|
Dans le cadre des séries, il reste à résoudre les schémas 4, 6 et 7, de même nature. La question se posera de toutes manières aussi avec l'alternance des coups, quelle est la bonne sstip pour 2 buts identiques non obligatoires ?
|
|
|
je veux bien essayer mais j'ai du mal à écrire un article... j'ai toujours le Circé mémoire en suspend... avec beaucoup de mal à mettre au point des diagrammes corrects :o) mais je veux bien tenter l'expérience.
à vous de juger en fonction de ce qui en découlera ! Merci en tout cas pour cette proposition.
Ceci dit la sstip est autant de toi que de moi. Ce n'est en rien un travail personnel mais plus une coopération. Pas de Cybernétique sans feed-back !
N.B. inédits veux dire qu'on ne les publie pas ici alors c'est ça?
|
|
|
je vais essayer de comprendre où ça pèche pour les 2 buts identiques non obligatoires ... c'est sans garantie mais je regarde !
|
|
|
Oui, la quasi-totalité des articles contient des inédits. D'une part ce sont des nouveautés qui stimulent la lecture (ne pas oublier que beaucoup de paires d'yeux sont braquées sur FE), et d'autre part ils participent au concours informel de l'année en cours de la revue, et les jugements font de la publicité pour le nouveau genre.
Par exemple pour l'aser, j'ai inclus des oeuvres provenant de FE mais aussi des inédits qu'on a mis en oeuvre sur le site privé de Cornel. D'ailleurs c'est une possibilité qu'on pourrait reprendre : finaliser les définitions dans le cadre des séries et demander à Cornel s'il accepterait d'ouvrir un workshop spécifique.
|
|
|
le Schéma 7 me pose un vrai problème.
en fait je ne vois pas comment imposer
1.Cf4 2.d4 3.dxc5 x
1.Cf4 2.d4 3.Cxh5 x
sans autoriser
1.Cb4 2.d4 3.dxc5 x
1.Cb4 2.Ca6 3.Cxc5 x
... et autres prises
en fait il faudrait compter les prises et pouvoir hiérarchiser celles ci pour trouver la variante la plus "prometteuse".
a) 1.Cf4 2.d4 permet "deux" prises (c'est la plus "prometteuse".)
b) d'autres variantes permet "une" prise
c) d'autres variantes permet "zero" prise.
ça me parait juste impossible avec une simple stipulation. la seule façon serait de créer "de novo" un nouveau but avec Popeye... et cela n'est possible que par programmation au sien d'un fonction propre dans Popeye.
je crois qu'il n'y a pas d'autre issue.
|
|
|
pour le reste :
nous pouvons adapter la sstip au nombre de buts voulus & à son caractère "facultatif" ou "obligatoire".
si l'on résume nous avons les deux "sstip" suivantes:
A & B buts facultatifs... : sstip white 3s[-1s[A] & -1s[B] | !-1s[!A|!B]]
A & B buts obligatoires: sstip white 3s[-1s[A] & -1s[B] & !-1s[!A&!B]]
du but unique :
A but facultatif... : sstip white 3s[-1s[A] | !-1s[!A]]
A but obligatoire : sstip white 3s[-1s[A] & !-1s[!A]]
au "quadruple but obligatoire" que tu as découvert dans le fil précédent que nous pouvons étendre au au "quadruple but facultatif", que nous n'avions pas encore envisagé, avec cette même modification:
quadruple but obligatoire: sstip white ns[-1s[+] & -1s[#] & -1s[x] & -1s[=] & !-1s[!+&!#&!x&!=]]
quadruple but facultatif... : sstip white ns[-1s[+] & -1s[#] & -1s[x] & -1s[=] | !-1s[!+|!#|!x|!=]]
cette dernière pourra figurer en bonne place dans le fil que vient d'ouvrir Jean Christian.
cette unité de présentation est rassurante et simplifiera la mémorisation. (cette sstipp est "généricable" ! )
|
|
|
sstip M buts n coups :
obligatoires: sstip white ns[-1s[A] & -1s[B] & ... & -1s[M] & !-1s[!A&!B]& ... &!M]]
facultatifs : sstip white ns[-1s[A] & -1s[B] & ... & -1s[M] | !-1s[!A|!B]| ... |!M]]
|
|
|
il faut cependant atténuer notre enthousiasme devant ces stipulations pour Popeye car contrairement aux buts pré-programmés, qui sont compilés au sein même du programme, ces stipulations ne peuvent qu'être interprétées par Popeye qui doit les "parser" à chaque boucle.
Le prix à payer sera donc un ralentissement considérable de la vérification!!
ainsi, si l'arbre des variantes est élevé il ne faut pas espérer confirmer le C+ d'un problème dont le nombre de coups est supérieur à 10 en un temps raisonnable. ( 10 coups sera déjà très lent à vérifier ) et cela croît avec le nombre de buts bien sûr.
cela sera différent quand ces buts seront programmés "dans Popeye" et compilés comme il se doit.
au moins nous avons un outils pour explorer cette nouvelle forme de problème.
|
|
|
Il reste une question à régler, soulevée par Jacques dans le fil précédent :
Schéma 9
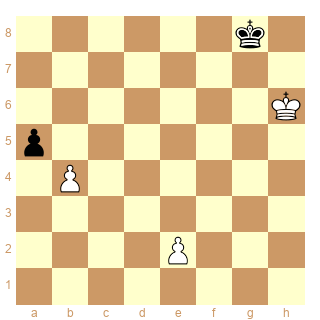
ser-(d+&dx)5
C'est C+ ou C- ?
Pour Popeye c'est C- à cause du dual D/T :
1.e2-e4 2.e4-e5 3.e5-e6 4.e6-e7 5.b4*a5 x
1.e2-e4 2.e4-e5 3.e5-e6 4.e6-e7 5.e7-e8=Q +
1.e2-e4 2.e4-e5 3.e5-e6 4.e6-e7 5.e7-e8=R +
Mais si un jour le but conjugué est programmé dans WinChloé ça sera C+ car, pour ce logiciel, le signe + signifie "échec mais pas mat", donc la solution avec la promotion Dame ne sera plus valide.
Je suggère de suivre Popeye pour 2 raisons :
- Il me semble plus naturel de considérer qu'un # réalise le but "+", puisqu'un mat est un échec particulier.
- On a pas besoin de modifier la sstip pour rendre C+ ce schéma 9.
Au moment d'envoyer je viens de me rendre compte qu'il n'est pas si clair que ce schéma 9 soit Popeye-démoli. En effet qu'est-ce qu'un problème démoli avec buts A et B (sachant qu'une solution réalise bien A et B) ?
1) Est-ce un problème avec 2 solutions réalisant chacune A et B (4 lignes dans Popeye) ?
2) Est-ce un problème avec 1 solution réalisant A et B et une autre qui réalise soit A soit B (3 lignes dans Popeye) ?
Mon "instinct" me pousse à décréter que la réponse est 2), donc que le schéma 9 est bien Popeye-démoli, mais c'est largement discutable...
Cet autre cas est aussi à trancher :
Schéma 10
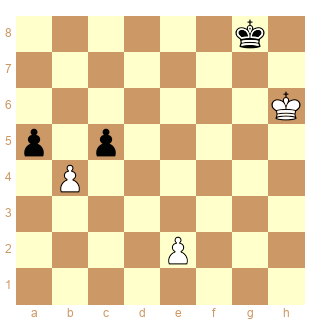
ser-(d#&dx)5
C'est C+ ou C- ?
1.e2-e4 2.e4-e5 3.e5-e6 4.e6-e7 5.b4*c5 x
1.e2-e4 2.e4-e5 3.e5-e6 4.e6-e7 5.b4*a5 x
1.e2-e4 2.e4-e5 3.e5-e6 4.e6-e7 5.e7-e8=Q #
Ici mon "instinct" me pousse encore à dire que c'est démoli (dual blanc). D'ailleurs si la stipulation était x1 (capture en 1 coup), ça serait considéré comme démoli (enfin il me semble...).
Bref, on pourrait établir comme régle que l'output de Popeye ne doit contenir que n lignes dans un problème avec n buts (sauf dans le cas de coups défensifs bien sûr, ainsi que dans le cas #&+ où on ne peut pas échapper aux 3 lignes puisque le mat est aussi un échec pour Popeye).
|
|
|
Il existe un autre cas critique, non encore examiné, celui où le même mouvement réalise les 2 buts.
Schéma 11
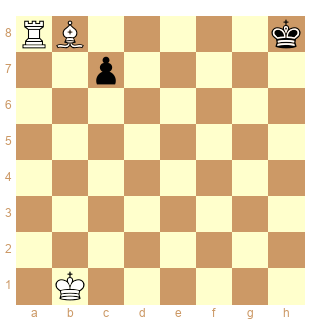
ser-(d#&dx)6 combien de solutions ?
Il est évident qu'il y a 1 ou 0 solution, selon que l'on accepte ou pas que le même mouvement réalise les 2 buts. Si on l'accepte, la solution est évidemment :
1.Kb1-c2 2.Kc2-d3 3.Kd3-e4 4.Ke4-f5 5.Kf5-g6 6.Bb8*c7 # x
Mais curieusement Popeye donne un output très zarbi dans cette situation :
1.Kb1-c2 2.Kc2-d3 3.Kd3-e4 4.Ke4-f5 5.Kf5-g6 6.Bb8*c7 + x
1.Kb1-c2 2.Kc2-d3 3.Kd3-e4 4.Ke4-f5 5.Kf5-g6 6.Bb8-a7 #
1.Kb1-c2 2.Kc2-d3 3.Kd3-e4 4.Ke4-f5 5.Kf5-g6 6.Bb8*c7 #
Alors je pense qu'il ne faut pas accepter une telle solution. Car d'une part ça évite ce genre d'output incompréhensible (pour moi !), et d'autre part un tel schéma 11 illustre en fait un problème "orthodoxe" avec commme but (unique) #&x.
Il faudra examiner de plus près l'échec à la découverte, qui risque de poser bien des difficultés...
|
|
|
Finalement je commence à douter qu'on ait raison de dire que le schéma 1 admette 2 solutions. Le dilemme est le suivant :
1) Un coup terminal réalise au moins A et un coup terminal différent réalise au moins B.
Ca c'est la définition sous laquelle le schéma 1 admet 2 solutions. Mais une autre définition est possible :
2) Un coup terminal réalise uniquement A et un coup terminal différent réalise uniquement B.
Sous cette définition, la suite
1.g4-g5 2.g5-g6 3.g6*f7 x
1.g4-g5 2.g5-g6 3.h6-h7 +
n'est plus une solution valide puisque g6*f7 x+ réalise les 2 buts en même temps.
Avec l'ancienne sstip white 2s[-1s[+] & -1s[x] & !-1s[+&x]], on avait bien uniquement la solution sans ambiguïté du schéma 1 :
1.Kc4-b5 2.Kb5-a6 3.Ka6*a7 x
1.Kc4-b5 2.Kb5-a6 3.h6-h7 +
Le problème de cette ancienne sstip est que la solution précédente n'est plus détectée au schéma 2. Par ailleurs la nouvelle sstip la détecte mais ajoute aussi la seconde solution au schéma 1...
Alors pour pouvoir trancher le dilemme (1 ou 2 solutions dans le schéma 1 ?) en toute sérénité, il nous faudrait une troisième sstip qui donne une unique solution à la fois pour le schéma 1 et le schéma 2, cette solution étant bien sûr :
1.Kc4-b5 2.Kb5-a6 3.Ka6*a7 x
1.Kc4-b5 2.Kb5-a6 3.h6-h7 +
Donc une sstip qui traduise la définition 2), un et un seul but réalisé par chaque coup terminal.
Tu peux nous trouvez ça Dominique ? Si non on gardera la définition 1).
|
|
|
Un truc marrant est qu'il existe une troisième définition possible (et pas idiote d'ailleurs), sous laquelle l'ancienne sstip fonctionne parfaitement :
3) Un coup terminal réalise uniquement A, un coup terminal réalise uniquement B, aucun coup terminal ne réalise à la fois A et B.
Sous cette définition le schéma 1 admet une unique solution et le schéma 2 aucune solution, ce qui est exactement le résultat donné par Popeye.
L'intérêt de cette définition 3) est qu'on est plus emmerdé par un coup réalisant plusieurs buts à la fois, dès que Popeye voit ça, il vire les solutions correspondantes de l'output.
Alors finalement je me demande si on ne devrait pas utiliser cette définition 3) et l'ancienne sstip, bien adaptée à ce cadre. C'est au moins une question qui se pose...
|
|
|
Voici un diagramme qui résume une bonne partie des choix possibles :
Schéma 12
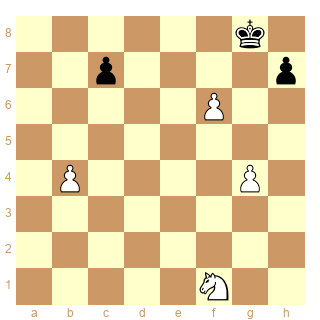
Les blancs peuvent faire échec et capturer en 3 coups de série, combien de solutions ?
Les 4 types de solutions sont présentes, et détectées par la sstip de Dominique white 2s[-1s[x] & -1s[+] | !-1s[!x|!+]]. En ce sens cette sstip est "maximale", elle détecte tout mais peut-être trop, c'est la question...
- Solution possible A, les 2 buts sont atteints par une même pièce, et par un même mouvement :
A : 1.g4-g5 2.g5-g6 3.g6*h7 + x
- Solution possible B, les 2 buts sont atteints par une même pièce, mais par des mouvements distincts :
B : 1.Sf1-e3 2.Se3-d5 3.Sd5*c7 x et 3.Sd5-e7 +
- Solutions possibles C et D, les deux buts sont atteints par deux pièces distinctes, chacune atteignant exactement un but.
C : 1.b4-b5 2.b5-b6 3.b6*c7 x et 3.f6-f7 +
D : 1.Sf1-e3 2.Se3-d5 3.Sd5*c7 x et 3.f6-f7 +
- Solution possible E, les deux buts sont atteints par deux pièces distinctes, l'une au moins atteignant les deux buts.
E : 1.g4-g5 2.g5-g6 3.g6*h7 + x et 3.f6-f7 +
Reste à trier le bon grain de l'ivraie...
|
|
|
Je n'ai pas eu le temps de lire tout le fil, Nico, mais il ne me semble pas que le fait que ce soit la même pièce (ou le même mouvement) ou 2 pièces distinctes (ou 2 mouvements distincts) qui réalisent les buts ait une quelconque importance.
Les solutions A et E sont simplement fausses (dépassons le stade de l'"impures") par chevauchement de but (avec g6*h7), et ne devraient pas apparaitre dans l'output de popeye avec une stip idéale.
Les autres solutions sont ok.
Mais, bon, je débarque là, et j'ai peut-être loupé des trucs.
|
|
|
[ prise et echec et (echec ou prise) et non (echec et prise)] ::: B C D
ce qui traduit en sstip donne :
sstip white 2s[ -1s[x] &-1s[+] & -1s[x|+] & !-1s[x&+]]
donne les solutions suivantes ( aux redondances près ):
1.b4-b5 2.b5-b6 3.b6*c7 x ( C )
1.b4-b5 2.b5-b6 3.f6-f7 + ( C )
1.Sf1-e3 2.Se3-d5 3.Sd5*c7 x ( B & D )
1.Sf1-e3 2.Se3-d5 3.f6-f7 + ( D )
1.Sf1-e3 2.Se3-d5 3.Sd5-e7 + ( B )
"Les solutions A et E sont simplement fausses" dixit J.C. ... alors cette formulation doit vous convenir
je ne vois pas encore comment distinguer ( par sstip) les cas A & E. car il n'y est plus question de distinguer "les buts" mais "les pièces atteignant ces buts".
N.B. evidemment si nous avions un opérateur ^ "ou exclusif" en plus du | "ou inclusif" la stipulation serait plus légère du type :
sstip white 2s[ -1s[x] &-1s[+] & -1s[x^+]]
|
|
|
C'est une façon de voir qui se tient, c'est clair, mais attention toutefois au mat : Popeye considère que c'est aussi un échec, donc si une sstip évacue les "solutions" A et E (comme le fait la première sstip d'ailleurs), elle ne détectera jamais de solutions pour le couple +# de buts...
D'autre part j'ai mentionné la possibilité de 2 énoncés différents, An&Bn et (A&B)n disons, le premier pour 2 pièces distinctes, chacune atteignant un des buts A et B, le second pour une même pièce qui atteint à la fois les buts A et B.
Je pense qu'il est important de garder cette distinction, reflétée d'ailleurs par les 2 exemples introductifs de ton propre fil.
Ainsi le schéma 12 admettrait exactement une solution, la B, sous l'énoncé ser-d(x&+)3, et admettrait exactement deux solutions, les C et D, sous l'énoncé ser-(dx&d+)3.
Bien entendu ce cadre serait celui de la "pureté maximale", puisqu'on ne considèrerait que le minimum de solutions valides. Il faut encore y réfléchir mais à priori ce n'est pas une possibilité idiote...
|
|
|
La première sstip donne ça aussi, Dominique. Le problème est que ça ne donnera plus rien avec les buts + et #.
La difficulté est qu'on ne veut pas la solution E, mais qu'on doit l'avoir dans le cas + et # :
E : 1.g4-g5 2.g5-g6 3.g6-g7 + # et 3.f6-f7 +
Si tu arrives à trouver une sstip qui vire E sauf lorsque le but A est "inclus" dans le but B (comme le # est inclus dans le +), je t'offre le champagne !
|
|
|
- Solution possible E, les deux buts sont atteints par deux pièces distinctes, l'une au moins atteignant les deux buts.
cela peut être isolé de la façon suivante :
sstip white 2s[ -1s[x] &-1s[+] & -1s[x&+|+]]
1.g4-g5 2.g5-g6 3.g6*h7 + x
1.g4-g5 2.g5-g6 3.f6-f7 +
toujours aux redondances près
|
|
|
. je dis des bêtises.
la sstip précedente est juste :
sstip white 2s[ -1s[x] &-1s[+] & -1s[x&+]]
rien de plus .
( elle isole E ... et toute variante contenant au moins une fois échec & prise. ce qui est logique)
|
|
|
Je pense qu'on sera tous d'accord pour dire que le mat ne réalise qu'un but (lui-même), et pas le double but +#.
Mais quid de l'échec double ? Le plus simple et cohérent serait de raisonner comme pour le mat, en disant que ++ ne réalise qu'un seul but (lui-même).
Et un coup à la découverte qui réalise en même temps un échec et un mat ?
Peut-être qu'une façon globale de s'en sortir serait de poser comme règle qu'un coup donné ne réalise qu'un seul but (au minimum d'occuper sa case d'arrivée !). Par exemple le but réalisé par g6xf7+ serait (zf7,x,+), considéré comme un seul but !
|
|
|
j'aurais tendance à penser également que si le but est atteint la solution est légitime... même s'il entraîne la réalisation d'un autre but en corollaire.
comme si je devais garder une glace au frais et chauffer ma cuisine.
mon frigo réalise très bien le premier but
un radiateur réalise très bien le second.
cependant le mode de fonctionnement de mon frigo fait que pour garder la glace au frais il turbine un max et chauffe aussi ma cuisine.
Il réalise les deux buts... il n'empêche qu'il remplit bien "sa" mission !
en deux mots :
1.g4-g5 2.g5-g6 3.g6*h7 + x me parait légitime.
si le but fixé est d'occuper la case h7 on ne peut opposer à la réalisation de ce but qu'il est infirmé par un echec... voire un mat ... et au prix d'une capture de surcroît !
"et pourtant il occupe h7!" aurait argué Galilé... avant de vendre son radiateur.
|
|
|
Donc tu n'es pas pour la "pureté maximale", piste que JC et moi-même explorons... Ainsi pour toi le schéma 12 admettrait :
- les solutions B et A sous l'énoncé ser-d(x&+)3.
- les solutions C, D et E, sous l'énoncé ser-(dx&d+)3.
C'est bien ça ?
|
|
|
oui, ça ne me dérangerais pas !
la beauté devant résider dans le problème qui offre de belles solutions plus que dans les contraintes imposées aux solutions.
A ² B seraient tous deux admis comme ser-d(x&+)3 mais la composition d'un problème de type B resterait bien plus méritoire à mon goût.
c'est purement subjectif! ce n'est qu'un avis.
mais il faut poursuivre la recherche de sstip spécifiques et ne pas décider en fonction de leur manque. Ce sont deux problèmes indépendants.
pour refuser le mat dans une recherche d’échec pur il suffit de remplacer "+" par "+&!#" mais il faut que le solutionniste soit prévenu de cette "entorse à l’échec" car si nous nous posons cette question c'est que le choix pourra sembler arbitraire par un tiers.
sstip white 2s[ -1s[x] & -1s[+&!#] & !-1s[x&+]]
nous avons bien les solutions sans mat !
tout comme les solutions sans "échec sur prise" propre à ce double but x & +!
1.b4-b5 2.b5-b6 3.b6*c7 x C
1.b4-b5 2.b5-b6 3.f6-f7 + C
1.Sf1-e3 2.Se3-d5 3.f6-f7 + D
1.Sf1-e3 2.Se3-d5 3.Sd5*c7 x D
1.Sf1-e3 2.Se3-d5 3.Sd5*c7 x B
1.Sf1-e3 2.Se3-d5 3.Sd5-e7 + B
reste à trouver comment séparer B (le bon grain) de C & D (l'ivraie )
mais je ne vois pas comment "séparer prise par une même pièce" & "prise par deux pièces distinctes"
|
|
|
Buts exclusifs [ (A ou B) mais non (A et B)]
sur le plan de deux buts A & B exclusifs l'un de l'autre nous devons les traiter comme deux buts dérivés P & Q tels que P= (A & !B) et Q= (B & !A)
notre sstip générique " sstip white ns[ -1s[P] &-1s[Q] & -1s[P & Q]] " devient donc : sstip white ns[ -1s[A&!B] & -1s[B&!A] & -1s[(A&!B)&(B&!A)]]
dans le cas des deux buts exclusifs [+ ; #] "i.e. échec (sans mat) ; mat"
+ sera (+&!#) et # sera (#) ( (#&!+) n'ayant pas de sens aux échecs)
la sstip correspondante sera : sstip white ns[ -1s[+&!#] &-1s[#] & -1s[(+&!#)& #]]
dans le cas des deux buts exclusifs [x ; +] "i.e. prise et échec "
la sstip correspondante sera : sstip white ns[ -1s[x&!+] &-1s[+&!x] & -1s[(x&!+)|(+&!x)]]
mais si l'on veut ici encore distinguer l'échecs du mat !! il faut encore préciser que + sera (+&!#) "i.e. prise et échec (sans mat!) "
la sstip correspondante sera alors : sstip white ns[ -1s[(+&!#) &!x ] &-1s[x&!(+&!#) ] & -1s[(x&!(+&!#) )|((+&!#) &!x)]]
|
|
|
je ne devrais pas poster en pleine nuit car les stipps ci dessus sont erronnées : les voici corrigées :
notre sstip générique " sstip white ns[ -1s[P] &-1s[Q] & !-1s[P & Q]] " devient donc :
sstip white ns[ -1s[A&!B] & -1s[B&!A] & !-1s[(A&!B)&(B&!A)]]
dans le cas des deux buts exclusifs [+ ; #] "i.e. échec (sans mat) ; mat" la sstip sera :
sstip white ns[ -1s[+&!#] &-1s[#] & !-1s[(+&!#)& #]]
dans le cas des deux buts exclusifs [x ; +] "i.e. prise et échec " la sstip sera :
sstip white ns[ -1s[x&!+] &-1s[+&!x] & !-1s[(x&!+)&(+&!x)]]
et si l'on veut ici encore distinguer l'échecs du mat !! la sstip sera alors :
sstip white ns[ -1s[(+&!#) &!x ] &-1s[x&!(+&!#) ] & !-1s[(x&!(+&!#) )&((+&!#) &!x)]]
|
|
|
Finalement on pourrait couper la poire en 2 :
- Ne pas accepter la "solution" A dans le cadre où la même pièce réalise plusieurs buts. La raison de fond est que cette solution est "orthodoxe" puisque ce n'est qu'un coup qui réalise le but +x.
- Accepter la solution E dans la cadre où des pièces différentes réalisent les buts. La raison de fond est que si on ne l'accepte pas, on sera toujours emmerdé par le # qui réalise 2 buts, le mat et l'échec.
La terminologie pourrait être "buts multiples" pour une pièce, et "buts conjugués" pour plusieurs pièces. Il me semble que c'est "causant".
Si on reprend le schéma 12, on aurait alors :

a) ser-(dx&d+)3, 3 solutions C+
b) ser-d(x&+)3, 1 solution C+
a) 1.b4-b5 2.b5-b6 3.b6*c7 x et 3.f6-f7 +
1.Sf1-e3 2.Se3-d5 3.Sd5*c7 x et 3.f6-f7 +
1.g4-g5 2.g5-g6 3.g6*h7 x et 3.f6-f7 +
b) 1.Sf1-e3 2.Se3-d5 3.Sd5*c7 x et 3.Sd5-e7 +
Qu'en pensez-vous ?
|
|
|
Je suis un peu perdu dans toutes tes sstips, Dominique... Si, comme je le suggère, on construit 2 théories, les buts multiples (une seule pièce thématique) et les buts conjugués (autant de pièces thématiques que de buts), il faut absolument trouver 2 sstips, l'une qui cible les buts multiples et l'autre qui cible les buts conjugués.
En effet, si on a un énoncé du type "buts multiples" en 50 coups, mais avec déjà des solutions "buts conjugués" en 2 coups, if faut absolument une sstip "buts multiples" spécifique, sinon l'output va exploser...
Voici un nouveau schéma qui illustre cela :
Schéma 13
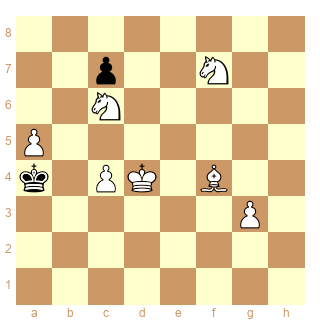
ser-h(x&+)12
Attention c'est du ser-h, donc du sstip black [1s]. La solution que j'ai en tête est 10.Rxc6 12.Rb8 Fxc7+ et il y a plein de solutions "buts conjugués" comme 2.Rc2 Cb4+ Fxc7
Alors est-ce que tu peux trouver une sstip qui isole le "but multiple", Dominique, afin
de pouvoir vérifié un tel schéma 13 ?
|
|
|
isoler les buts multiples A & B .
black (n-1)s[ 1s[A&B] & !1s[A&!B] & !1s[B&!A]]
ce qui apliqué au Schéma 13 donne :
Pieces
White Sf7 Sc6 Pa5 Pc4 Kd4 Bf4 Pg3
Black Pc7 Ka4
sstip black 12s[ 1s[+&x] & !1s[+&!x] & !1s[x&!+]]
Option movenum
black 12s[ 1s[+&x] & !1s[+&!x] & !1s[x&!+]] 7 + 2
1 (Ka4-b4 Time = 0.015 s)
2 (Ka4*a5 Time = 0.015 s)
3 (Ka4-a3 Time = 0.015 s)
4 (Ka4-b5 Time = 0.015 s)
5 (Ka4-b3 Time = 0.015 s)
1.Ka4-b3 2.Kb3-c2 3.Kc2-d1 4.Kd1-e2 5.Ke2-f3 6.Kf3-g4 7.Kg4-f5 8.Kf5-e6 9.Ke6-d7 10.Kd7*c6 11.Kc6-b7 12.Kb7-b8 Bf4*c7 +
1.Ka4-b3 2.Kb3-c2 3.Kc2-d1 4.Kd1-e2 5.Ke2-f3 6.Kf3-g4 7.Kg4-f5 8.Kf5-e6 9.Ke6-d7 10.Kd7*c6 11.Kc6-b7 12.Kb7-b8 Bf4*c7 + x
solution finished. Time = 0.015 s
la réponse est bien unique ...
et "La solution que (tu as ) en tête" est bien C+
|
|
|
Ca c'est super, bravo ! Et pour le contraire ? je veux dire sur un diagramme avec une longue solution "buts conjugués", tu sais l'isoler pour qu'elle ne soit pas parasitée par plein de courtes solutions "buts multiples" ? Par exemple :
Schéma 14
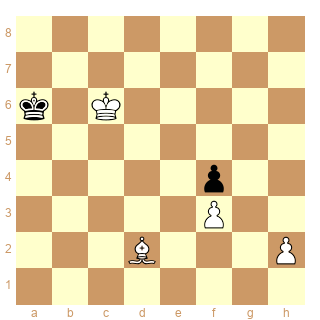
ser-(hx&h+)8
Solution en tête : 7.Rg5 8.F*f4 x h4+
Attention, ici j'ai pris la définition du but conjugué qui autorise qu'un des coups atteigne les 2 buts (Fxf4 x+). Comme déjà indiqué si on autorise pas ça, on ne pourra jamais travailler avec le mat et l'échec, puisque le mat réalise aussi l'échec.
Il y a une solution en 1 avec buts multiples : 1.Ra7 Fe3+ Fxf4
|
|
|
Ça ne va pas :
BeginProblem
sstip black 11s[ 1s[+&x] & !1s[+&!x] & !1s[x&!+]]
Protocol C:popeye....
Pieces
White Sb7 Pc4 Kd4 Bf4
Black Pc7 Ka4
Option movenum
EndProblem
donne :
1 (Ka4-b4 Time = 0.040 s)
2 (Ka4-a5 Time = 0.040 s)
3 (Ka4-a3 Time = 0.040 s)
4 (Ka4-b5 Time = 0.040 s)
5 (Ka4-b3 Time = 0.040 s)
1.Ka4-b3 2.Kb3-c2 3.Kc2-d1 4.Kd1-e2 5.Ke2-f3 6.Kf3-g4 7.Kg4-f5 8.Kf5-e6 9.Ke6-d7 10.Kd7-c8 11.Kc8-b8 Bf4*c7 +
1.Ka4-b3 2.Kb3-c2 3.Kc2-d1 4.Kd1-e2 5.Ke2-f3 6.Kf3-g4 7.Kg4-f5 8.Kf5-e6 9.Ke6-d7 10.Kd7-c8 11.Kc8-b8 Bf4*c7 + x
6 (c7-c5 + Time = 0.070 s) 7 (c7-c6 Time = 0.070 s)
et pas ... 10.Kd7-c6 11.Kc6-b6... à cause du coup 11...c5+ (échec et pas prise)
|
|
|
ici je ne vois pas 'angle d'attaque:
a) autant pour le cas précédent (schéma 13 )le problème est simple puisque les deux buts sont atteints au même moment ( même pièce & coup unique 12...Bf4*c7 +x )
b) autant pour le cas suivant (schéma 14 ) le problème me parait insoluble par sstip puisque les deux buts sont atteints par la même pièce en deux coups différents [1...Bd2*f4 x; 1...Bd2-e3 +]
conclusion: dès lors que l'on exclu l'atteinte simultanée des buts "+x" pour une atteinte séparée des buts "+;x" le fait que cela soit atteint par deux pièces différentes ou par une pièce unique est absolument indiscernable par une sstip ( à ma connaissance )
je dis pas que ce n'est pas possible, je dis que je ne vois pas comment l'obtenir par sstip!
|
|
|
@Jacques: 11...c5+ (échec et pas prise)
dans le shéma 13, nous recherchons la première occurence "d'échec et prise" simultanée!
11...c5+ doit être accompagné d'une prise pour être une démolition
la prise isolée ou l'échec isolés sont ignorés.
D'ailleurs dans la version de Nicolas le coup 10.Kd7*c6 est bien une prise qui n'interfère pas avec la solution.
ta version du problème me parait être aussi correcte que celle proposée par Nicolas.
ceci dit, le fait que la sstip nous donne ici ce que nous en attendons n'est pas un gage de fiabilité à tout crin.
Et si elle est démolie il, vaut mieux s'en rendre compte dès maintenant.
|
|
|
pour illustrer cette histoire de "sstip trompeuse" j'ai trouvé ce "monstre incorrect" !
Pieces
White Sf7 Sc6 Pa5 Pc4 Kd4 Bf4 Pg3
Black Pc7 Ka4
sstip black 12s [ 1s[x&!+] &1s[+&!x] & !1s[(x&!+)&(+&!x)] &! (1s[(+&!#) &!x ] &1s[x&!(+&!#) ] & !1s[(x&!(+&!#) )&((+&!#) &!x)])]
Option movenum
EndProblem
1 (Ka4-b4 Time = 0.015 s)
2 (Ka4*a5 Time = 0.031 s)
3 (Ka4-a3 Time = 0.031 s)
4 (Ka4-b5 Time = 0.031 s)
5 (Ka4-b3 Time = 0.031 s)
1.Ka4-b3 2.Kb3-c2 3.Kc2-d1 4.Kd1-e2 5.Ke2-f3 6.Kf3-g4 7.Kg4-f5 8.Kf5-e6 9.Ke6-d7 10.Kd7*c6 11.Kc6-b7 12.Kb7-a6 13.Ka6*a5 Bf4*c7 + x
solution finished. Time = 0.031 s
c'est le même problème que celui de Nicolas, et cette sstip tordue trouve une solution en 13 coups mais occulte totalement la solution de Nicolas.
il est donc important que nous contrôlions nos sstip .... en premier lieu en vérifiant qu'elles reposent sur une logique compréhensible par tous.
black (n-1)s[ 1s[A&B] & !1s[A&!B] & !1s[B&!A]]
voilà une formulation assez simple à analyser... elle semble à priori isoler le double but simultané... y voyez vous une erreur de raisonnement ? si non! est elle prise en défaut dans un problème vérifiable? c'est encore possible... n'hésitez pas à l'infirmer.
la stipp tordue du début de ce post par contre est un monstre puisque que sa solution est démolie par la précédente... je l'avais pourtant construite de façon (que je croyais) logique. attention donc!
|
|
|
Jacques à raison. Il y a erreur dans cette sstip !
son exemple criant!
|
|
|
re OOps! la sstip fait bien ce qu'on lui demande! je viens de comprendre l'erreur.
la position proposée par jacques est la suivante.
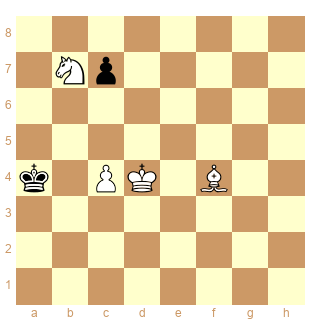
la solution est bien unique
1.Ka4-b3 2.Kb3-c2 3.Kc2-d1 4.Kd1-e2 5.Ke2-f3 6.Kf3-g4 7.Kg4-f5 8.Kf5-e6 9.Ke6-d7 10.Kd7-c8 11.Kc8-b8 Bf4*c7 + x
en effet :
1.Ka4-b3 2.Kb3-c2 3.Kc2-d1 4.Kd1-e2 5.Ke2-f3 6.Kf3-g4 7.Kg4-f5 8.Kf5-e6 9.Ke6-d7 10.Kd7-c6 ?? 11.Kc6-b6 et ( 11...c5+ ; 11...Bf4*c7 x ) echec ; puis echec & prise
nous avons ici les deux but atteints spar deux pièces différentes , et nous demandons à la sstip de ne pas les considérer comme des démolitions car elle ne sont pas attendues !
n'est ici démolition "qu'échec & prise simultanées." ( i.e. par une même pièce au même coup )
ce que recherche Nicolas est [ une sstip qui isole le "but multiple"]
je crois que celle ci n'est pas encore rejettée.
j'espère que tu es d'accord Jacques?
|
|
|
puisque nous y sommes ! la complémentaire à cette sstip ( donner une sstip qui évite le "but multiple")
ne pas avoir (A & B) tout en ayant (A & !B) et (!A & B)
sstip black (n-1)s[!1s[+&x] & 1s[x&!+] & 1s[+&!x]]
position de Nicolas : schéma 13
Pieces
White Sf7 Sc6 Pa5 Pc4 Kd4 Bf4 Pg3
Black Pc7 Ka4stip black 1s[!1s[+&x] & 1s[x&!+] & 1s[+&!x] ]
une solution en un coup.
1.Ka4-a3 Bf4-c1 +
1.Ka4-a3 Bf4-d6 +
1.Ka4-a3 Bf4*c7 x
position de Jacques : diagramme ci dessus.
Pieces
White Sf7 Sc6 Pa5 Pc4 Kd4 Bf4 Pg3
Black Pc7 Ka4
sstip black 1s[!1s[+&x] & 1s[x&!+] & 1s[+&!x] ]
trois solutions en un coup.
1.Ka4-b4 Bf4-d2 +
1.Ka4-b4 Bf4-d6 +
1.Ka4-b4 Bf4*c7 x
1.Ka4-a3 Bf4-c1 +
1.Ka4-a3 Bf4-d6 +
1.Ka4-a3 Bf4*c7 x
1.Ka4-b3 Sb7-a5 +
1.Ka4-b3 Sb7-c5 +
1.Ka4-b3 Bf4*c7 x
Au total les deux sstip sont :
sstip black (n-1)s[ 1s[+&x] & !1s[+&!x] & !1s[x&!+]] : pour isoler le but multiple
sstip black (n-1)s[!1s[+&x] & 1s[x&!+] & 1s[+&!x] ] : pour éviter le but multiple
|
|
|
llustration:
schéma 15.
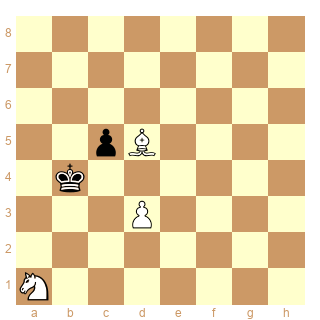
Pieces
White Bd5 Pd3 Sa1
Black Pc5 Kb4
isoler le but multiple
sstip black 3s[ 1s[+&x] & !1s[+&!x] & !1s[x&!+]]
1.c5-c4 2.Kb4-c5 3.Kc5*d5 d3*c4 + x
1.c5-c4 2.c4-c3 3.c3-c2 Sa1*c2 + x
éviter le but multiple
sstip black 1s[!1s[+&x] & 1s[x&!+] & 1s[+&!x] ]
1.c5-c4 Sa1-c2 +
1.c5-c4 Bd5*c4 x
1.c5-c4 d3*c4 x
Evidement cela ne répond pas au schéma 14 ... mais comment séparer lescoups de deux pièces différentes?
Pieces
White Kc6 Pf3 Bd2 Ph2
Black Ka6 Pf4
éviter le but multiple : sstip black 1s[!1s[+&x] & 1s[x&!+] & 1s[+&!x] ]
1.Ka6-a7 Bd2-e3 +
1.Ka6-a7 Bd2*f4 x
isoler le but multiple : sstip black 2s[ 1s[+&x] & !1s[+&!x] & !1s[x&!+]]
1.Ka6-a7 2.Ka7-b8 Bd2*f4 + x
|
|
|
notez que dans la position ci-dessus le pion d3 ( outre le fait de proposer une seconde solution )empèche une prise multiple comme
1.Kb4-a3 2.c5-c4 3.Ka3-a2 Bd5*c4 +x ::: en raison de la variante :
1.Kb4-a3 2.c5-c4 3.Ka3-a2 d3*c4 x ::: le but multiple n'est plus isolé
il s'agit de la même raison qui empèche la démolition 10.Kd7-c6 ?? ..( 11...c5+ ; 11...Bf4*c7 x+ ) dans la position proposée par Jacques.
|
|
|
Pour s’y retrouver, il faut donner des définitions des buts multiples et conjugués, et des noms aux sstips correspondantes. Il nous en faut 4, selon qu’on travaille en but facultatif ou obligatoire, en buts multiples ou conjugués. Notons-les respectivement sstipBMF, sstipBCF, sstip BMO et sstipBCO. On note aussi A et B les buts.
Définition des buts multiples :
- Un mouvement d’une pièce X réalise au moins le but A.
- Un mouvement différent de la même pièce X réalise au moins le but B.
La sstipBMF doit donc détecter ce cas de figure, mais ne doit pas détecter :
- Un mouvement unique d’une pièce X qui réalise A et B (y compris par une découverte).
- Un mouvement d’une pièce X qui réalise au moins le but A et un mouvement d’une pièce différente Y qui réalise au moins le but B.
Donc pour contrôler la validité de sstipBMF, il faut un diagramme avec :
- Une « solution courte » avec un mouvement unique d’une pièce X qui réalise A et B.
- Une « solution courte » avec un mouvement d’une pièce X qui réalise A et un mouvement d’une pièce différente Y qui réalise B.
- Une solution longue avec un mouvement d’une pièce X qui réalise A et un mouvement différent de la même pièce X qui réalise B.
La sstipBMF ne doit alors détecter que la solution longue, donc ne pas être parasitée par les autres.
Définition des buts conjugués :
- Un mouvement d’une pièce X réalise au moins le but A.
- Un mouvement d’une autre pièce Y réalise au moins le but B.
La sstipBCF doit donc détecter ce cas de figure, mais ne doit pas détecter :
- Un mouvement unique d’une pièce X qui réalise A et B (y compris par une découverte).
- Un mouvement d’une pièce X qui réalise au moins le but A et un mouvement différent de la même pièce X qui réalise au moins le but B.
Donc pour contrôler la validité de sstipBCF, il faut un diagramme avec :
- Une « solution courte » avec un mouvement unique d’une pièce X qui réalise A et B.
- Une « solution courte » avec un mouvement d’une pièce X qui réalise A et un mouvement différent de la même pièce X qui réalise B.
- Une solution longue avec un mouvement d’une pièce X qui réalise A et un mouvement d’une autre pièce Y qui réalise B.
La sstipBMF ne doit alors détecter que la solution longue, ne pas être parasitée par les autres.
Il me semble que la sstip [1s[A&B] & !1s[A&!B] & !1s[B&!A]] est le bon candidat pour sstipBMF. En effet elle colle avec le schéma 13 et aussi avec celui de Jacques, puisqu'elle ne détecte pas sa solution à buts conjugués (et c'est ce qu'on veut !) :
10.Kd7-c6 11.Kc6-b6 (c5+ et Bf4*c7 x)
Maintenant il faudrait trouver sstipBCF, qui donc fasse le contraire sur la diagramme de Jacques, détecter
10.Kd7-c6 11.Kc6-b6 (c5+ et Bf4*c7 x)
Mais ne pas détecter
10.Kd7-c8 11.Kc8-b8 (Bf4*c7 + x)
Si c'est impossible on va être à la peine, la seule possibilité restante que je vois étant alors de considérer
10.Kd7-c8 11.Kc8-b8 (Bf4*c7 + x)
non plus comme une fausse solution mais comme une démolition. Comme ça si l'output présente de telles solutions courtes à buts multiples, l'auteur n'a pas besoin de fouiller dans tout l'output pour trouver sa solution à buts conjugués, car son problème est considéré démoli.
Dit autrement, un but conjugué serait "strict", i.e. démoli par un but multiple.
Cette possibilité à une certaine logique interne : si on demande que deux pièces fassent chacune la moitié du job, on peut aussi demander en plus l’impossibilité qu’une pièce fasse tout le job à elle toute seule.
Par souci d’homogénéité, on pourrait même demander que le but multiple soit aussi « strict ». Comme ça on est plus emmerdé par les sstip, il suffit de garder [1s[A] & 1s[B] | !1s[!A|!B]].
Si la plus courte solution détectée est en buts conjugués sans buts multiples, c’est C+ en buts conjugués, et uniquement dans ce cas. Si cette plus courte solution détectée est en buts multiples sans buts conjugués, c’est C+ en buts multiples, et uniquement dans ce cas.
Maintenant il faut voir en pratique si c’est jouable. Ce qui est certain est que c’est nickel-chrome du point de vue de la sstip, unique pour chaque type d’énoncé, multiple ou conjugué.
|
|
|
Si l’on suit mon idée précédente, le futur article pourrait contenir le passage suivant :
Nous avons décidé que les deux genres « buts multiples » et « buts conjugués » étaient mutuellement exclusif. La raison est d’ordre pratique, nous n’avons en effet pas su trouver deux s-stipulations de Popeye, l’une isolant le but multiple, l’autre le but conjugué.
Si donc un but conjugué n’était pas une démolition pour un but multiple (et réciproquement), la vérification grâce à Popeye serait rendue très difficile dans le cas d’un problème admettant une solution courte conjuguée et une solution longue multiple. En effet l’output correspondant serait parasité par la répétition, pour chaque nombre de coups, de la solution conjuguée, rendant problématique la preuve de l'unicité de la solution multiple.
Mais bien entendu, si une procédure d’isolation des buts multiples/conjugués nous avait échappé, ou bien était programmée à l’avenir, rien n’empêcherait d’introduire les concepts de buts multiples/conjugués non mutuellement exclusifs. Pour cette raison, notre théorie se nomme buts multiples/conjugués « stricts », en attendant une éventuelle nouvelle théorie « relative ».
|
|
|
.
|
|
|
je pense que c'est la solution la plus sage.
un problème à "buts conjugués" sera toujours plus court qu'un problème à "buts multiples" ( à position identique )
si un problème présente une solution en conjugué il suffit de le passer au crible de la sstip "multiple" dans le même nombre de coups pour se rendre compte qu'il n'y aura, le plus souvent, pas de réponse. ( et donc C+ ) les rares solutions en un nombre de coups identique seront alors des démolitions pour le problème conjugué !
partant de là nous avons deux sstip permettant de créer et de vérifier le C+ buts multiples et buts conjugué comme tus les rappelles :
buts multiples : sstip black (n-1)[1s[A&B] & !1s[A&!B] & !1s[B&!A]]
buts conjugués : sstip black (n-1)[1s[A] & 1s[B] | !1s[!A|!B]]
pour la distinction entre conjugué par même pièce ou par pièces différentes je ne vois aucune issue par stipp! il faut ici créer des fonctions propres à POPEYE.
|
|
|
"un problème à "buts conjugués" sera toujours plus court qu'un problème à "buts multiples" ( à position identique )"
Pourquoi ? le schéma 14 n'est-il pas un buts multiples en 1 coup et un buts conjugués en 7 coups ?
Si on suit mon idée (une solution "buts multiples" est une démolition à l'énoncé "buts conjugués", et une solution "buts conjugués" est une démolition à l'énoncé "buts multiples) ne peut-on pas garder uniquement la sstip
[1s[A] & 1s[B] | !1s[!A|!B]] ?
En effet, à moins que j'ai loupé quelque chose, cette sstip détecte à la fois les buts multiples et les buts conjugués. Donc il suffit de regarder la première liste de "solutions" de l'output (pour le nombre minimal de coups) et :
- s'il ne contient que du but multiple, c'est C+ multiple et C- conjugué.
- s'il ne contient que du but conjugué, c'est C+ conjugué et C- multiple.
- s'il contient à la fois du but multiple et du but conjugué, c'est C- multiple et C- conjugué.
A noter qu'un coup qui réalise les 2 buts (comme un mat qui réalise toujours un échec), est toujours la moitié d'une solution en "buts multiples" (auquel cas un autre coup de la même pièce doit la compléter) et aussi la moitié d'une solution en "buts conjugués" (auquel cas un coup d'une autre pièce doit la compléter).
|
|
|
Schéma 16
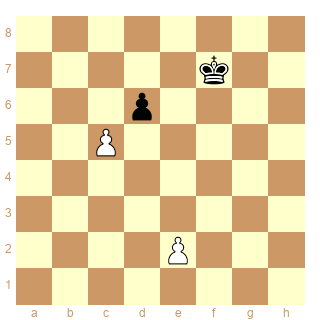
Si on suit ma proposition (« buts multiples » et « buts conjugués » mutuellement exclusif), alors il n'y a aucun ser-(dx&d+) valide ni aucun
ser-d(x&+) valide ! En effet, en utilisant uniquement la sstip white 2s[-1s[x] & -1s[+] | !-1s[!x|!+]], l'output donne une solution en buts multiples :
1.e2-e4 2.e4-e5 3.e5*d6 x
1.e2-e4 2.e4-e5 3.e5-e6 +
Il donne aussi une solution de même longueur en buts conjugués :
1.e2-e4 2.e4-e5 3.c5*d6 x
1.e2-e4 2.e4-e5 3.e5-e6 +
Et comme les 2 genres sont mutuellement exclusif (l'un est incorrect si l'autre est présent et vice-versa), ces 2 solutions sont invalides !
|
|
|
ok! je trouve cela cohérent.
comment classer par ailleurs ce petit problème "conjugo-multiple" !
shéma 17
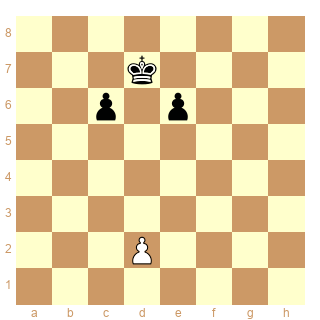
1.d2-d4 2.d4-d5 3.d5*e6 + x
1.d2-d4 2.d4-d5 3.d5*c6 + x
les deux solutions sont multiples!
« buts multiples » à deux solutions
cependant ces deux solutions réalisent ensemble les « buts conjugués » de manière croisées.
bien sûr, je dirais démolis comme toi je pense car une sstip ne recherchant que les « buts conjugués » ne verraient pas ces solutions que l'humain voit!
|
|
|
bah c'est « buts multiples » dans les deux cas de figure ! le stipps me perburbent ! il me faut un break :o)
|
|
|
Houla ! Il va me falloir 3 jours pour lire tout ça. Guère de temps en ce moment. Et guère doué en informatique pour piger quelque chose à toutes ces stips.
Toutefois, sur vos 2 derniers posts, je crois avoir compris l’essentiel. Il est évidemment normal que la présence d’une solution en buts multiples invalide la solution en buts conjugués. Et vice-versa. Admettre la validité des 2 solutions coexistantes serait une hérésie.
Mais, vous le savez, ce que je préfère c’est composer et résoudre, et je trouve que ce fil manque un peu de compositions pour l'agrémenter.
Alors voici un petit problème que je trouve assez mignon dans sa simplicité et son économie. Je pense être dans le sujet : il s’agit bien de buts facultatifs et non de buts obligatoires.

ser-d(#&+&x&=)7 2 solutions C+
Pas sûr de l’énoncé, mais ça devrait être ça.
Je vous laisse le résoudre (sans popeye, hé !).
2 remarques :
- la stip classique (sans doute dépassée maintenant) liste impeccablement les 8 solutions, auxquelles elle ajoute les 2 mats comptabilisés aussi comme échecs.
Pas trop grave, on l’a dit, mais ça m’énervait tout de même. Alors, en modifiant un peu, je suis tombé sur une stip qui ne comptabilise plus le mat en tant qu’échec, mais qui, curieusement, affiche 2 fois l’échec sans mat. Je préfère déjà, mais ça demeure un peu gênant. Ne peut-on supprimer cette stupide répétition ? Voici la stip en question :
sstip white 7s[-1s[+&!#] & -1s[#] & -1s[x] & -1s[=] & !-1s[+&!# & # & x & =]]
Mais sans doute avez-vous déjà découvert tout cela plus haut dans le fil.
- ce problème est à buts multiples, puisque c’est la même pièce qui fait les 4 boulots. Mais comme ce sont 2 pièces différentes qui effectuent le travail, il y a un vague parfum de conjugaison dans l’histoire. Je plaisante évidemment ; ce sont 2 solutions distinctes en buts multiples, mais c’est amusant tout de même.
Bon, mais il faut que j’épluche vos travaux, car il y a un truc à la base que je ne parviens pas à comprendre. Mais je ne veux en parler qu’en connaissance de cause.
|
|
|
Ce schéma 17 est un cas très intéressant ! A part le "buts multiples" et le "buts conjugués", j'ai mentionné qu'une troisième théorie est possible, celle nécessitant un seul mouvement d'une même pièce réalisant les 2 buts. Mais cette théorie est "orthodoxe", c'est juste la théorie classique (un seul mouvement terminal) où le but à atteindre est A&B.
Donc je ne trouve pas pertinent de développer cette troisième théorie, puisqu'elle existe déjà, au moins en filigrane...
Pour en revenir au schéma 17, il admet donc 2 solutions "orthodoxes" avec but unique +x, ça c'est clair. Il admet 0 solutions en "buts conjugués", c'est clair aussi puisqu'il faut au moins 2 pièces blanches pour réaliser un buts conjugués !
La question est de savoir s'il admet 1 solution ou 2 solutions avec "buts multiples". C'est à dire si ce que tu appelles "solution(s) croisée(s)" compte pour 1 ou 2.
Cas 1 solution :
1.d2-d4 2.d4-d5 3.d5*e6 +
1.d2-d4 2.d4-d5 3.d5*c6 x
On fait un choix en disant par exemple que l'échec est par la droite et la capture par la gauche...
Cas 2 solutions :
1.d2-d4 2.d4-d5 3.d5*e6 +
1.d2-d4 2.d4-d5 3.d5*c6 x
1.d2-d4 2.d4-d5 3.d5*e6 x
1.d2-d4 2.d4-d5 3.d5*c6 +
On ne fait pas de choix, une solution correspond à l'échec par la droite et une autre à l'échec par la gauche.
Pour le moment je ne vois pas d'argument solide permettant de trancher... Au feeling je dirais 2 solutions, car je me souviens d'un débat théorique qui préconise de dire que les mouvements d5*e6 + et d5*e6 x sont en fait distincts...
C'est le genre de question qu'il faudrait poser sur un workshop...
|
|
|
Jean Christian :
cette sstip donne ce que tu désires il me semble ! pas de répétition 1#, 1+, 1x & 1= dans chaque solution ( ni double + ni double # )
sstip white 7s[-1s[#|+] & -1s[x] & -1s[=] & !-1s[+ & x & =]]
à noter que dans !-1s[+ & x & =] le # n'est pas nécessaire; comme aucun échec ne sera accepté aucun mat ne passera.
|
|
|
@ JC
Moi ce que je préfère c'est composer à l'intérieur d'un cadre solide, j'ai trop peur que mes travaux s'avèrent ensuite être hors des clous ! En pratique ça a failli arriver avec mon 1er Prix circé mémoire, heureusement que l'inventeur (qui se reconnaitra !) a "à posteriori" modifié son réglement pour que cette oeuvre entre dans le cadre !
Que l'on soit bien d'accord avec les implications de la préconisation actuelle :
Schéma 18
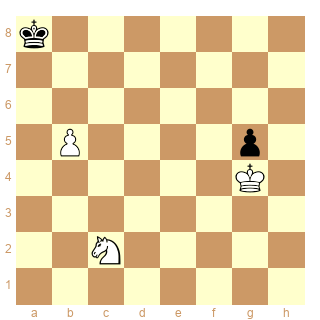
Ceci est un ser-(d+&dx)2 (buts conjugués) valide, avec comme solution :
1.b6 2.b7+ R*g5 x
Mais ce n'est pas un ser-d(+&x)3 (buts multiples) valide, malgré la "solution" :
1.Cd4 2.Ce6 3.Cc7+ Cxg5 x
En effet la préconisation actuelle est de seulement regarder le début de l'output (nombre minimal de coups) avec la sstip
[-1s[x] & -1s[+] | !-1s[!x|!+]]. Ce début est :
1.b5-b6 2.Kg4*g5 x
1.b5-b6 2.b6-b7 +
C'est la solution en 2 coups pour le but conjugué, qui implique "de facto" que tout ce qui suit dans l'output est invalide, en particulier la "solution" en 3 coups pour le but multiple.
On est bien sur la même longueur d'onde ?
|
|
|
je suis d'accord avec la nécessité de définir un cadre bien verrouillé! sinon il y aura des oppositions voire un rejet de la condition à terme.
la solution la plus courte est une démolition pour toute solution plus longue, que les buts soient multiples ou conjugués!
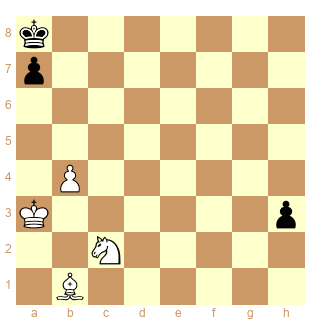
ser-d(+&x)2 3 solutions (buts multiples)
1.b4-b5 2.b5-b6 3.b6*a7 x
1.b4-b5 2.b5-b6 3.b6-b7 +
1.Sc2-d4 2.Sd4-b5 3.Sb5*a7 x
1.Sc2-d4 2.Sd4-b5 3.Sb5-c7 +
1.Bb1-a2 2.Ba2-e6 3.Be6*h3 x
1.Bb1-a2 2.Ba2-e6 3.Be6-d5 +
|
|
|
le problème de Jean Christian réalise la moitié du task (AUW et AUW-buts multiples)
c'est du haut vol!
|
|
|
"la solution la plus courte est une démolition pour toute solution plus longue, que les buts soient multiples ou conjugués!"
Et même plus : le solution la plus courte en buts conjugués est une démolition pour toute solution de même longueur en buts multiples, et vice-versa !
Schéma 19
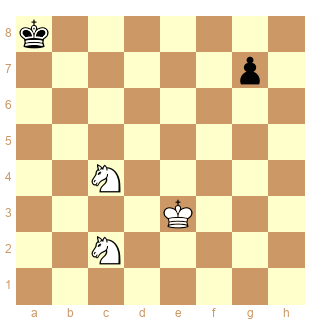
C- en buts multiples
C- en buts conjugués
Il y a deux "solutions" en buts multiples :
1.Sc4-d6 2.Sd6-e8 3.Se8*g7 x
1.Sc4-d6 2.Sd6-e8 3.Se8-c7 +
1.Sc2-d4 2.Sd4-e6 3.Se6*g7 x
1.Sc2-d4 2.Sd4-e6 3.Se6-c7 +
Mais on peut les "conjuguer" (dans l'esprit de la remarque de JC plus haut), pour obtenir une "solution" en buts conjugués :
1.Sc2-d4 2.Sd4-e6 3.Se6*g7 x
1.Sc2-d4 2.Sd4-e6 3.Sc4-b6 +
Résultat des courses, tout ce petit monde s'auto-annihile, plus aucune solution n'est valable, ni en conjugué ni en multiple !
PS : je viens de recevoir une réponse de Bojan (il était en vacances la semaine dernière), il a aussi trouvé la stip
[-1s[A] & -1s[B] | !-1s[!A|!B]], je vais lui demander s'il est possible de la scinder en 2 pour isoler le cas multiple et le cas conjugué.
|
|
|
C'est magie d'internet de faire se rencontrer les esprits forturés ;0)
j'imagine Bojan comme un fan d'Edgar Alan Poe!
N.B le shéma 19 est très didactique! il faut le conserver :)
|
|
|
@Dominique
Merci beaucoup! C'est exactement ce que je cherchais dans l’immédiat.
PS : mon problème marche aussi avec le pion b2 en d2. Mêmes solutions, mais avec promotions en d8 au lieu de b8, un discriminant insuffisant pour en faire des jumeaux ;o)
@Nico
Bien sûr. Ce sont là des évidences.
Mais je vais dire une connerie là (je n'ai toujours pas lu l'intégralité du fil!): je ne vois pas la nécessité de distinguer dans l'énoncé buts conjugués et buts multiples. Même si ce distinguo existe évidemment dans la pratique du genre. C'est compliquer les choses et donner au solutionniste une indication superflue qui facilite la recherche.
C'est au compositeur de s'arranger pour qu'une solution (qu'elle soit en buts multiples ou en buts conjugués, cela relève de son choix) soit unique, plus courte que les autres, et remplisse les conditions en termes de nombre de coups.
Et si 2 solutions sont possibles (une en multiple, l'autre en conjugué, ou plusieurs en multiple et plusieurs en conjugué) le problème est faux tout simplement, sauf si on a précisé "2 ou n solutions".
En cas de solution « mixte » (par exemple une pièce réalise 3 buts et une autre le dernier but), on retombe en fait dans le cas de buts conjugués. Solution valide si c’est la seule et la plus courte, mais à déconseiller car impure de but.
Un seul et même énoncé devrait donc suffire. Une seule et même stip aussi. Ca simplifierait drôlement les choses. Avec comme principe : toute solution unique plus courte que les autres est la solution valide.
Toutefois, il est vraisemblable, je m'en doute, que j'ai loupé des propos évoquant des cas de figure qui justifient ce distinguo dans l'énoncé. Ou alors peut-être est-il impossible d’écrire une stip qui chapeaute toutes les formes envisageables?
Pouvez-vous me renseigner sur ce sujet et me prouver que j’ai perdu une belle occasion de me taire ?
|
|
|
Allez je te fais un petit topo rapide !
On a une sstip qui détecte à la fois les buts conjugués et les buts multiples, c'est :
[-1s[A] & -1s[B] | !-1s[!A|!B]]
(on enlève les "-" si le trait change au coup terminal bien sûr).
Alors je suis d'accord que si on n'a que cette sstip à disposition, on peut associer les 2 genres en un seul.
Mais imagine un gars qui fait un sublime "buts multiples" en 100 coups, mais avec une putain de solution "buts conjugués" en 2 coups qu'il arrive pas à éradiquer ?
C'est pourquoi je préconise qu'on continue à chercher un couple de sstip, l'une qui ne détecte que les buts multiples (sstipBM) et l'autre que les buts conjugués (sstipBC). Comme ça le gars peut vérifier son 100 coups avec sstipBM (il ne peut pas le faire avec la sstip actuelle car l'output va exploser), et déclarer qu'il a construit un "buts multiples" valide en 100 coups, mais qui n'est plus valide si on associe les 2 genres.
De manière générale, je pense qu'on pourrait nous reprocher de ne pas distinguer les 2 genres, quitte à en introduire un troisième qui associe les 2...
|
|
|
Ah j'ai peut-être une bonne idée : ajouter le genre comme condition féerique (c'est d'ailleurs une condition féerique).
Par exemple h+x3 est orthodoxe, l'unique coup terminal doit à la fois faire échec et capturer (but unique +x). Dans notre cadre on aurait des énoncés du style :
h+x=#3 +x buts multiples, =# buts conjugués.
Comme ça on aurait toute la panoplie possible...
|
|
|
Schéma 18 bis

a) ser-(+x)2 buts conjugués
b) ser-(+x)3 buts multiples
Solutions :
a) 1.b6 2.b7+ R*g5 x
b) 1.Cd4 2.Ce6 3.Cc7+ C*g5 x
Bien entendu une telle théorie "dissociée" ne pourra être viable que si on trouve les 2 sstips qui dissocient les 2 genres...
|
|
|
@ Dominique
Mauvaise nouvelle, il y a un problème avec ta sstip :
[-1s[A] & -1s[B] | !-1s[!A|!B]]
En effet elle détecte aussi les cas où le même mouvement réalise les 2 buts.
Et c'est embêtant car si par exemple on a cette possibilité au diagramme et qu'une solution (en conjugué ou en multiple) demande beaucoup de coups, l'output va exploser... Par exemple :
begin
pieces white Ba8 Pd2 black Kc8 Bb7
sstip white 3s[-1s[x] & -1s[+] | !-1s[!x|!+]]
end
1.d2-d4 2.Ba8*b7 + x
1.d2-d4 2.Ba8*b7 +
1.d2-d3 2.Ba8*b7 + x
1.d2-d3 2.Ba8*b7 +
1.d2-d4 2.d4-d5 3.Ba8*b7 + x
1.d2-d4 2.d4-d5 3.Ba8*b7 +
1.d2-d3 2.d3-d4 3.Ba8*b7 + x
1.d2-d3 2.d3-d4 3.Ba8*b7 +
1.d2-d4 2.d4-d5 3.d5-d6 4.Ba8*b7 + x
1.d2-d4 2.d4-d5 3.d5-d6 4.Ba8*b7 +
1.d2-d4 2.d4-d5 3.d5-d6 4.d6-d7 +
1.d2-d3 2.d3-d4 3.d4-d5 4.Ba8*b7 + x
1.d2-d3 2.d3-d4 3.d4-d5 4.Ba8*b7 +
La solution n'est pas détectée au début de l'output, je crains donc qu'il ne faille te remettre à l'ouvrage pour parfaire ta sstip...
Si c'est impossible, il nous restera heureusement la proposition de JC, de mettre dans le même sac buts conjugués, buts multiples, mais aussi "buts par le même mouvement".
|
|
|
Ok, Nico. Je vois ton idée.
Sans être vraiment convaincu.
Car le problème, à mon avis, c’est que tu cherches à « dissocier les deux genres », comme tu dis, alors qu’ils n’en font qu’un, même s’il manque un terme générique qui recouvre les deux.
Disons qu’il s’agit de « problèmes à buts associés » qui se subdivisent en « problèmes à buts multiples » et « problèmes à buts conjugués ». Mais cette subdivision est artificielle et n’est perçue que par notre œil de compositeur mais ne peut logiquement pas l’être par l’œil de popeye, du moins en apparence.
Alors c’est un peu comme si, à l’intérieur du genre mat direct, tu cherchais à dissocier les mats donnés par le fou, par le cavalier, etc… ou les mats donnés à la découverte, les mats donnés avec une prise, etc… ou que sais-je encore.
Dans l’exemple que tu cites, celui du « buts multiples en 100 coups » empêché par « un buts conjugués en 2 coups », c’est comme si tu râlais parce que ton #100 que tu comptais administrer avec un fou est pourri par un #2 donné par un cavalier. A toi de te démerder pour éliminer le « buts conjugués en 2 coups » ou le #2 du cavalier. Par contre la présence, dans ces deux mêmes problèmes, d’un s#4 ne te gênera pas parce qu’il s’agit d’un autre genre que la stipulation ne prend pas en compte.
Or, je le répète, on est en présence ici, à mon sens, d’un genre unique, à l’intérieur duquel il serait vain, voire inintéressant, de vouloir discriminer. Car quel intérêt, pour garder l’analogie avec le direct, d’essayer de programmer popeye pour lui demander un #2 donné par le roi à la découverte ? A part d’éliminer tous les #1 qui te gênent ? Trop facile, et pour toi et pour le solutionniste.
Dans tous les cas, c’est trop en demander au nouveau-né que nous essayons de dorloter.
Alors, en l’absence des 2 sstips dissociantes, le mieux serait peut-être de considérer, pour l’instant au moins, que nous évoluons dans un genre unique et compact, en nous débrouillant pour avoir des outputs impeccables. Ce n’est pas le boulot qui manque.
Mais, bon, tu me connais, j’écris ça maintenant après quelques instants de réflexion (avec un tas de gens qui gueulent autour de moi), mais j’aurais peut-être changé d’avis dans une heure ;o)
|
|
|
Erratum à la dernière ligne :"j'aurai".
|
|
|
Bien entendu je suis parfaitement d'accord pour regarder de plus près le genre "buts associés", d'autant plus qu'on a du mal à trouver les sstips adéquates pour bien discriminer.
Mais alors je constate immédiatement une difficulté : est-ce qu'on pousse l'idée à fond, en ajoutant la possibilité que plusieurs buts soient atteints par le même mouvement ?
- Si oui, le cadre (+,#) pose problème puisqu'un mat est toujours un échec. En particulier toutes les entrées de type "G" sont démolies, car il suffit de 3 mouvements pour les obtenir (#,=,x).
- Si non, d'une part ça manque d'homogénéité (pourquoi confondre "buts multiples" et "buts conjugués" et laisser à part "buts par le même mouvement" ?), et d'autre part la sstip détecte les buts par le même mouvement (voir mon post précédent).
So what ?
|
|
|
nicolas! ça ne va pas être simple :o)
mais pour l'instant, sur ton exemple j'ai cet axe de recherche, partant de ta dernière position :
sstip white 3s[ -1s[+&x] & !-1s[+&!x] & !-1s[x&!+]]
1.d2-d4 2.Ba8*b7 + x
1.d2-d3 2.Ba8*b7 + x
1.d2-d4 2.d4-d5 3.Ba8*b7 + x
1.d2-d3 2.d3-d4 3.Ba8*b7 + x
1.d2-d3 2.d3-d4 3.d4-d5 4.Ba8*b7 + x
sstip white 3s[ !-1s[+&x] |-1s[+&!x] | -1s[x&!+]]
1.d2-d4 2.Ba8*b7 + x
1.d2-d4 2.d4-d5 3.Ba8*b7 + x
1.d2-d3 2.d3-d4 3.Ba8*b7 + x
1.d2-d4 2.d4-d5 3.d5-d6 4.Ba8*b7 + x
1.d2-d4 2.d4-d5 3.d5-d6 4.d6-d7 +
1.d2-d3 2.d3-d4 3.d4-d5 4.Ba8*b7 + x
sstip white 3s[!-1s[!x] & !-1s[!+] & -1s[!+&!x] | -1s[+&!x] | -1s[x&!+]]
1.d2-d4 2.d4-d5 3.d5-d6 4.d6-d7 +
je vais travailler la dessus et essayer de trouver une sstip plus adéquate.( et concise )
|
|
|
Pour le cas de la conjugaison # + je pense qu'on peut les dissocier en précisant [+&!#] pour l'échec . Il faudra une sstip spécifique mais j'ai le sentiment que c'est jouable.
|
|
|
Pas vraiment un problème, Nico.
Je ressens les buts atteints par un même mouvement comme une impureté (et même une incorrection) basique du genre. On peut éventuellement les traiter comme une bizarrerie à part, encore que je ne sois pas convaincu de l'intérêt de la chose.
Il faut les virer du corpus "buts associés", en précisant simplement dans notre définition de départ que tous les buts (multiples et conjugués) doivent être atteints par un mouvement distinct (= qui réalise un seul but, sans faire double emploi, donc).
A mon avis ça n'enlève rien à l’homogénéité de l'ensemble et j'ai même le sentiment que ça la renforce. Ce n'est pas le nombre des éléments impliqués mais leur cohérence interne parfaite qui fait l'homogénéité d'un ensemble. Dehors le vilain petit canard!
La stip les détecte? Ok, mais à condition qu'ils existent. Au compositeur de se débrouiller pour qu'ils soient absents du problème, en respectant par cette contrainte la définition qu'on aura donnée au départ.
|
|
|
@ JC
Si on met tout dans le même sac, en posant : "buts associés" = "buts multiples" ou "buts conjugués" ou "buts par le même mouvement", on va tomber sur des saletés comme ça :
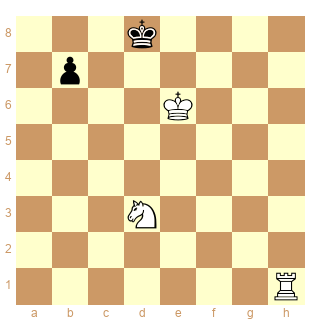
a) Direct-2, buts associés +x
b) Direct-2, buts associés +#
a) 1.Cc5 2.C*b7 +x
b) 1.Rd6 2.Th8 +#
Tout le monde sera d'accord que le a) réalise bien les 2 buts demandés, mais on va nous prendre pour des malades si on dit que le b) réalise bien les 2 buts demandés, et pourtant c'est vrai !
Le hic est qu'il est sous-entendu, quand on demande de réaliser les buts + et #, qu'un coup donne mat et qu'un autre coup donne juste échec...
On pourrait suivre la piste de Dominique, remplacer les 2 buts + et # par +&!# et #, mais alors il deviendrait quasi-impossible de réaliser ces 2 buts par un même mouvement, sauf une découverte. Pourquoi pas, après tout ?
Oups croisement, donc tu ne veux pas inclure le cas où le même mouvement réalise les 2 buts.
"tous les buts (multiples et conjugués) doivent être atteints par un mouvement distinct (= qui réalise un seul but, sans faire double emploi, donc)"
Là je crois que c'est trop strict, tu te places dans le cas où le schéma 1 n'admettrait pas la solution
1.g5 2.g6 3.h7 +
1.g5 2.g6 3.g*f7 x+
Et on sera toujours coincé par le cas du mat qui réalise toujours aussi l'échec...
|
|
|
Après avoir pesé le pour et le contre, il me semble finalement qu’on aurait intérêt à aussi inclure, dans la théorie des « buts associés », le double but atteint par un même mouvement.
Le pour :
- Une meilleure homogénéité.
- Le genre « buts associés » devient intéressant pour les non féeristes, qui peuvent s’amuser avec des buts doubles, du style mat sur la case f5, mais en restant dans le champ orthodoxe (un seul coup atteint les 2 buts).
- La sstip est maintenant parfaite puisqu’elle détecte les 3 possibilités du genre « buts associés ».
Le contre :
- En composant en buts multiples ou buts conjugué, on peut être gêné par la troisième possibilité du genre « buts associés », mais elle est tellement spécifique qu’en pratique ça devrait aller.
- Le mat qui réalise toujours un double but en un seul coup. On peut s’en sortir avec l’astuce de Dominique, travailler avec # et +& !# plutôt qu’avec # et +. Cela force bien deux mouvements distincts, même un mat à la découverte où la pièce qui bouge fait échec n’est pas considéré par Popeye comme atteignant le double but # et +& !#.
Votre avis ?
|
|
|
Bonsoir, je vois les choses très simplement (peut-être comme J.-C.).
ser-ABCn. A, B et C désignent trois buts.
Après toutes les séries de zéro (position de départ pour un ser-ABC1), 1,2 , ...n-1 coups, on pose trois questions :
- Existe-t-il maintenant au moins un coup blanc qui atteint le but A ?
- Existe-t-il maintenant au moins un coup blanc qui atteint le but B ?
- Existe-t-il maintenant au moins un coup blanc qui atteint le but C?
Si on répond oui aux trois questions, on a une solution (c'est-à-dire un ensemble de coups qui résout le problème, autrement dit solution = solution de l'auteur ou démolition). On note qu'un même coup peut faire l'affaire pour plusieurs question. Une solution est donc une série ramifiée à son extrémité terminale, avec un bouquet final d'un nombre quelconque de fleurs. Si le nombre de fleurs est supérieur à trois : dual/démolition, en règle générale.
Comme toujours, si une solution ne plaît pas à l'auteur, c'est une solution parasite (démolition), et c'est à l'auteur de l'éliminer (et non à la règle qui dirait, par exemple, qu'une démolition doit avoir la même forme qu'une belle solution...).
Quant à (+ sans mat) vs (+ avec mat), c'est une autre histoire.
|
|
|
pour le cas(+ sans mat) vs (+ avec mat):
je pense que ns[-1s[+&!#] & -1s[#]] est absolument correct :
par ailleurs : [!(+&!#)|!#]] signifie [!+ & !# | #] qui est une tautologie et peut donc être ignorée :
la sstip pour (+ sans mat) vs (+ avec mat) est donc simplement :
ns[-1s[+&!#] & -1s[#]]
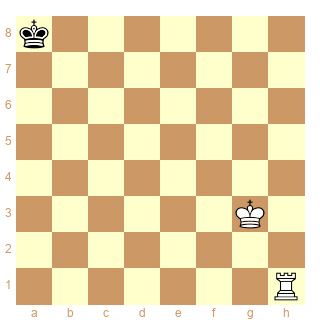
Pieces
White Kg3 Rh1
Black Ka8
sstip white 4s[-1s[+&!#] & -1s[#]]
1.Kg3-f4 2.Kf4-e5 3.Ke5-d6 4.Kd6-c7 5.Rh1-h8 +
1.Kg3-f4 2.Kf4-e5 3.Ke5-d6 4.Kd6-c7 5.Rh1-a1 #
|
|
|
@ Jacques
"On note qu'un même coup peut faire l'affaire pour plusieurs question".
Tu te places alors dans le cadre que je viens de défendre, où un même coup qui réalise les 3 buts (mat par capture sur f7 par exemple) est une solution. Dans ce cadre je viens d'écrire aussi une définition, équivalente ou presque :
Dans le genre « buts associés A&B», le coup terminal doit satisfaire à l’un des trois critères suivants :
- Atteindre simultanément les buts A et B (buts simultanés).
- Etre composé d’un coup atteignant au moins A et d’un coup différent de la même pièce atteignant au moins B (buts multiples).
- Etre composé d’un coup atteignant au moins A et d’un coup d’une autre pièce atteignant au moins B (buts conjugués).
Dans le cas où le but A est « inclus » dans le but B (comme le mat est « inclus » dans l’échec), les deux buts seront considérés comme étant A et B/A (B mais pas A).
Le genre « buts associés A&B» est vérifiable par Popeye sous la s-stipulation suivante, qui détecte simultanément les trois critères possibles :
[1s[A] & 1s[B] | !1s[!A|!B]]
|
|
|
@ Dominique
Oui la sstip marche pour le cas # et +/#. La question délicate est plutôt de savoir si on considère que le mat ne réalise que le mat, ou s'il réalise aussi l'échec.
Par exemple dans un problème où il faut atteindre(#,+), est-ce que un seul coup matant est une solution viable ? On a envie de dire que non, c'est pourquoi je suggère au-dessus de stipuler qu'en fait (#,+) signifie (#,+&!#). Comme ça il faut 2 coups pour atteindre (#,+), ce n'est pas vérifié pour un seul coup matant.
|
|
|
cela marche égalemnt en cas d'échecs ( ou mat ) à la découverte.
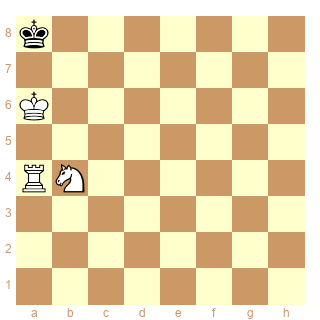
Pieces
White Ka6 Ra4 Sb4
Black Ka8
sstip white 1s[-1s[+&!#] & -1s[#]]
1.Sb4-c6 2.Ka6-b5 +
1.Sb4-c6 2.Ka6-b6 #
Popeye signale bien sûr le doublon [ 1.Sb4-c6 2.Ka6-b5 + ] en rapport "l'échec" & "l'échecs qui ne fait pas mat"... c'est le même échec mais nous demandons à Popeye de le tester deux fois !!
c'est juste le problème du compositeur ( lors de la vérification du C+ ) cette redondance n'existe pas pour le solutionniste .
je suis d'accord avec vous pour dire que la correction du problème est d'abord l'affaire du compositeur.
croisement : oui, le mat signifiera toujours échecs! Il faut donc spécifier un but ( échec non mat )
un problème réalisant les deux buts sur un même coups ( échec à la découverte ) ne pose un problème que sur un échecs double par les deux pièces d'une même batterie... j'avoue que je n'ai pas testé mais en toute logique, la sstip exigera un nouvel échec pour avaliser le problème. ( l'échec double n'est pas testé ici )
|
|
|
il n'existe pas de test pour l'echec double [++] apparemment , sinon:
sstip white ns[-1s[+&!#] & -1s[#] | -1s[#&++]] serait une bonne candidate
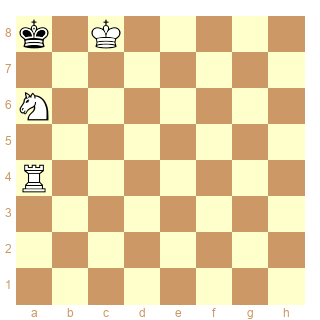
intention : 1.Cc7# ( ++) non détectée car mat isolé pour la sstip .
Pieces
White Kc8 Sa6 Ra4
Black Ka8
sstip white 4s[-1s[+&!#] & -1s[#]]
1.Ra4-b4 2.Sa6-c5 3.Rb4-b8 +
1.Ra4-b4 2.Sa6-c5 3.Rb4-a4 #
1.Ra4-b4 2.Rb4-b7 3.Rb7-a7 +
1.Ra4-b4 2.Rb4-b7 3.Rb7-b8 +
1.Ra4-b4 2.Rb4-b7 3.Sa6-c7 #
démoli car multiple & conjugué? mais ça reste un shéma pour l'échec double.
|
|
|
En fait, si finalement on adopte l'idée au-dessus, la seule différence entre un problème à un but (i.e. orthodoxe) et un problème à buts associés est que, plutôt que de demander un coup terminal qui réalise le but, on demande une liste de coups terminaux (n'importe laquelle) qui réalise tous les buts. Toi qui voulais une définition simple JC, te voilà servi !
Reste maintenant à définir un tel problème C+. En orthodoxe c'est facile, le coup réalisant le but doit être unique (du moins en "facultatif"). C'est quoi la généralisation, une liste strictement unique ?
Je ne vois pas d'objection à priori, juste la remarque que s'il existe une solution à buts simultanés (i.e. un seul élément suffit dans la liste), alors il est interdit qu'un autre coup atteigne l'un des buts, sinon on a une seconde liste à 2 éléments...
|
|
|
Juste un mot pour le cas de + et de #.
Je ne vois plus là aucun problème. En listant les buts à atteindre dans notre définition, on n'a qu'à préciser:
- échec ET mat (et non MAT ou échec AVEC mat; échec ET mat est d'ailleurs la formule consacrée , qui confirme bien le double but qu'on a toujours reconnu à ce coup particulier). L'échec et mat, où les 2 buts sont inéluctablement liés, ne réalise donc pas, à l'évidence, l'objectif simple échec (sans mat) tel qu'il peut être exigé par ailleurs, en tant que but spécifique. En outrepassant le simple échec, il constitue un but bien particulier.
- échec SANS mat (mais pas la peine, à mon avis, de préciser SANS mat, car la chose coule de source).
Pour le reste, on a la stip qui permet d'éviter le doublon dans l'output. Mais même si on ne l'avait pas et qu'il faille éliminer le doublon "à la main", je ne vois pas en quoi ça entacherait la correction d'une solution.
Mais Jacques a raison. Ne mâchons pas trop le travail au compositeur. C'est à lui à coller aux règles que nous édicterons; il n'a pas à réclamer des aménagements qui s'adapteraient à son problème incorrect pour le rendre correct.
Il nous faut désormais trancher.
Bon, maintenant, il reste d'autres points à régler, notamment celui du double but atteint par un même mouvement. J'ai donné mon avis là-dessus, mais on peut évidemment en discuter.
Holà! Croisement, Nico.
|
|
|
Ben, oui, ta définition me convient.
Au lieu de faire # en 2 coups, tu dois faire, disons, # et = en 2 coups. Ou #, =, + et x en 2 coups.
C'est aussi simple que ça, à mon avis.
Rien de féerique, c'est tout à fait orthodoxe dans mon esprit.
Mais je pige mal ton troisième paragraphe. Pourrais-tu l'expliciter et me donner un exemple?
|
|
|
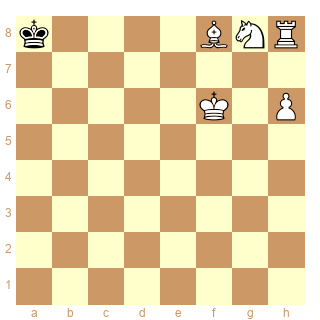
Pieces
White Bf8 Sg8 Rh8 Pf6 Ph6 Kb4
Black Ka8
sstip white 4s[-1s[+&!#] & -1s[#]]
1.Sg8-e7 2.Se7-c6 3.Sc6-a5 4.Bf8-d6 +
1.Sg8-e7 2.Se7-c6 3.Sc6-a5 4.Bf8-e7 +
1.Sg8-e7 2.Se7-c6 3.Sc6-a5 4.Bf8-g7 +
1.Sg8-e7 2.Se7-c6 3.Sc6-a5 4.Bf8-c5 #
1.Sg8-e7 2.Se7-c8 3.Bf8-c5 4.Sc8-a7 +
1.Sg8-e7 2.Se7-c8 3.Bf8-c5 4.Sc8-b6 +
1.Sg8-e7 2.Se7-c8 3.Bf8-c5 4.Sc8-e7 +
1.Sg8-e7 2.Se7-c8 3.Bf8-c5 4.Sc8-d6 #
exploitation d'une batterie plurielle T/F T/C
buts multiples #/+
1.Sg8-e7 2.Se7-c8 3.Bf8-c5 me plait beaucoup ! pour le réarrangement de la batterie T/C pour libérer le fou avant le mat.
|
|
|
@ JC
Suppose que tu veuilles réaliser les buts A, B et C et qu'un coup terminal X réalise les 3 buts en même temps. Si un autre coup terminal Y réalise au moins un des 3 buts c'est démoli, puisque la liste des coups réalisant les 3 buts n'est plus unique, elle contient (X) et (X,Y).
|
|
|
Dans cet esprit, mon dernier problème est alors démoli en raison des multiple échecs dans une même variante/solutions?
i.e: faut il aussi un échecs "seul" et un mat "seul"?
des multiples "singuliers" en somme :o)
ou alors , toute variante n'atteignant qu'un seul but est admise dans la mesure ou les autres buts sont atteints indépendamment.
|
|
|
Je n'y suis toujours pas, Nico.
Mon Dieu, que ce jargon de matheux est abscons! Je t'ai connu plus clair. Faut dire aussi que je suis vanné. Toi aussi, sans doute.
Comment un même coup terminal X pourrait-il réaliser 3 buts en même temps? A moins que tu ne comptes le mat comme 2 buts distincts (échec et mat), je ne vois pas. Mais on a bien dit que le mat ne devait pas être comptabilisé comme un échec. Alors liste-moi en clair 3 buts qui peuvent être atteints par un même coup. Échec, prise et pat, par exemple?????
D'autre part, je suis pour bannir les coups qui atteignent plusieurs buts, je l'ai déjà dit. Ils foutent la pagaille et n'enrichissent en rien le genre.
Mais de toute façon, c'est au compositeur à se démerder pour supprimer le coup terminal Y, tout simplement.
|
|
|
Si les buts sont par exemple #, x, za1, un unique coup peut mater en capturant sur a1...
"D'autre part, je suis pour bannir les coups qui atteignent plusieurs buts"
Ici je me range du côté de Dominique et de sa métaphore du frigidaire...
|
|
|
Ah, ok. Tu pinailles, là. Je m'en tenais aux 4 buts évoqués jusqu'à ce jour (+, #, =, x). C'est pourquoi je ne comprenais pas.
Toi-même tu parlais d'ailleurs d'AUW de but pour ces 4 là, ce qui semblait exclure l'admission d'autres buts dans la confrérie.
Tricheur! ;o)
C'est quoi cette histoire de frigidaire?
|
|
|
pour rappel :o) voici le siège de la métaphore du frigidaire
mais ce n'est qu'un avis... et je reste ouvert à toute discussion.
Pour tout dire, ce qui reste simple est plus judicieux... le compositeur doit faire en sorte que son problème ne souffre pas d’équivoque.
je suis sur que nous allons aboutir à un consensus! le bon sens devant prévaloir sur la démocratie! ( le nombre ne vaut pas la raison, à vous de choisir les lois :o)
il est vrai qu'avec le zug on peut rajouter au moins 64 nouveaux buts ! ^^
|
|
|
Rigolo ton histoire de frigo ;o)
Mais faux, à mon sens, quand on l'applique à ce qui nous intéresse, même si je n'ai plus la tête à t'expliquer mon raisonnement ce soir.
Quant au zug, on touche là aux auto-buts. Hors sujet donc. Dans mon esprit du moins.
Bonne nuit à tous les deux.
|
|
|
Bien entendu, je pense qu'ici tout le monde se fiche comme d'une guigne de savoir si ce sont ses idées ou celles des potes qui seront finalement retenues.
Dans un ordre décroissant d'importance, je dirais qu'il faut se soucier de :
1) La logique interne : il faut que quelle que soit la matrice et la stipulation, on puisse dire sans aucune ambiguïté si le problème est correct ou pas.
2) Le confort du lecteur : il faut qu'il sache exactement ce qu'il doit faire devant un tel problème, que sa tâche soit facilement mémorisable et que sa quête de la solution soit intéressante.
3) Le confort du compositeur : il doit pouvoir facilement cibler la stipulation correcte et la façon de vérifier son problème par un logiciel.
|
|
|
Merci. Avant un gros dodo moi aussi, je vais indiquer pourquoi considérer toutes les façons possibles et imaginables d'atteindre les buts me semble bonne :
1) Je ne vois aucun trou dans la logique interne, surtout après avoir remplacé + par +&!#. On regarde la liste L des coups terminaux, qui contient au moins une sous-liste S de coups réalisant l'ensemble des buts, puisque Popeye détecte L. Si L=S le problème est C+, il est démoli autrement. Si en plus on est en "inverse" (buts obligatoires), il suffit d'ajouter que c'est C+ si L=S=ensemble des coups terminaux légaux. Net et sans bavures.
2) Le lecteur sait de suite exactement quoi faire, trouver une position "pré-terminale" telle que l'ensemble des buts soit atteignable au coup suivant. Rien de plus simple à mémoriser, et de quoi bien s'amuser.
3) Aucun souci pour la stipulation, toujours la même condition féerique "buts associés" (c'est bien une condition féerique JC, mais il est inutile de nous lancer en ce moment dans un débat théorique à ce sujet). Aussi une sstip unique qui isole exactement le cadre. En plus le compositeur orthodoxe peut trouver chaussure à son pied en se restreignant au cas où tous les buts sont atteints par un même mouvement. S'il a des ennuis avec notre sstip, il en trouvera une qui isole la partie orthodoxe !
|
|
|
Tout gain de pièce est une capture ;-)
A = capture sans disparition de la pièce capturée. B = capture avec disparition de la pièce capturée = gain d'une pièce, symbole %.
ser-AB6 Circé
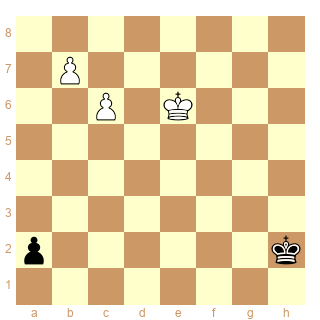
|
|
|
"échec ET mat (et non MAT ou échec AVEC mat; échec ET mat est d'ailleurs la formule consacrée , qui confirme bien le double but qu'on a toujours reconnu à ce coup particulier)."
Arrête-moi si je dis une connerie mais peut-il y avoir mat sans échec ? En extinction peut-être mais en général on veut juste faire mat quitte à le redéfinir non ?
|
|
|
l'idée de Jacques est vraiment étonnante! et son probnlème fonctionne.
je reste cependant étonné devant les résultats de Popeye pour le problème suivant (du même type ) dont la solution me laisse perplexe!
elle ne colle pas avec ma logique: faut il faire confiance en Popeye ici?
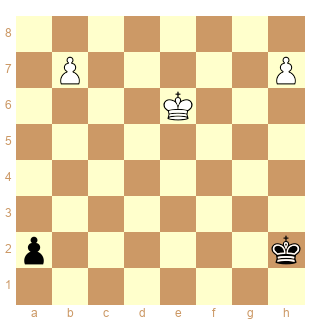
ser-%+ Circé
Pieces
White Pb7 Ph7 Ke6
Black Pa2 Kh2
sstip white 5s[-1s[!%&x] & -1s[%]] 3 + 2
condition Circe
1.h7-h8=B 2.Bh8-b2 3.b7-b8=R 4.Rb8-a8 5.Ra8*a2[+bPa7] (x) 6.Ra2*a7 (%)
a) pourquoi accepte t il cette solution?
b) pourquoi ne propose t-il mas la variante aussi douteuse mais équivalent suivante :
1.b7-b8=R 2.Rb8-a8 3.h7-h8=B 4.Bh8-b2 5.Ra8*a2[+bPa7] (x) 6.Ra2*a7 (%)
c) considère t-il que les buts atteints successivement sont solutions comme cela semble être le cas ici?
je reste dubitatif! quelle est mon erreur ,
|
|
|
Oops: il faut rester objectif! Popeye fera ce qu'on lui demande & rien de plus!
alors je me modère : faut il faire confiance en cette sstip ici ( et ailleurs )?
|
|
|
a) parce qu'elle est valide !
1.h7-h8=B 2.Bh8-b2 3.b7-b8=R 4.Rb8-a8 5.Ra8*a2 [+bPa7] 6.Bb2-a3 +
1.h7-h8=B 2.Bh8-b2 3.b7-b8=R 4.Rb8-a8 5.Ra8*a2 [+bPa7] 6.Ra2*a7 %
b) Si il la propose :
1.b7-b8=R 2.h7-h8=B 3.Rb8-a8 4.Bh8-b2 5.Ra8*a2 [+bPa7] 6.Ra2*a7 %
c) Les buts ne sont pas atteints successivement, la capture avec renaissance ne vérifie pas %.
Donc pas de souci, la sstip marche ici sans problème !
A ce propos est-ce qu'il existe une sstip qui isole le cas "orthodoxe" (tous les buts réalisés par le même mouvement) ?
|
|
|
Bien joué, Jacques!
Observons qu'on peut faire des jumeaux avec le pion a2 en b2 ;o)
Dominique, je ne sais pas. La sstip ne semble pas convenir dans ce cas. Mais ça, c'est ton domaine et tu vas régler le problème vite fait ;o)
|
|
|
Pardon! Pas de jumeaux, parce que alors on peut faire tour en b8.
|
|
|
Oui la double promotion Dame fait toujours son effet ! Par contre, ser-AB6 signifie qu'un 6ème coup atteint le but AB (cas orthodoxe). Il faut ajouter la condition féerique "Buts associés", sinon l'énoncé n'a pas de solution...
|
|
|
Merci Nicolas! C'est donc bien ma logique était en défaut!
Et encore bravo à Jacques pour cette belle idée!
|
|
|
oops ,Nicolas:
1.h7-h8=B 2.Bh8-b2 3.b7-b8=R 4.Rb8-a8 5.Ra8*a2 [+bPa7] 6.Bb2-a3 + n'atteind pas le but. Il faut une prise sans renaissance au même coup non?
Ici il ne s'agit que d'un échec qui ne fait pas partie des buts!
|
|
|
Ton énoncé est ser-%+, pas ser-%x.
D'ailleurs on peut signaler un problème de spécificité avec le couple de buts % x.
En effet % signifie annihilation (capture sans renaissance), tandis que x signifie annihilation ou capture avec renaissance.
Pour que l'output ne risque pas d'exploser, il faut donc utiliser les buts spécifiques % et x&!%.
|
|
|
Oui il existe une confusion pour l'énoncé, mea culpa, mais pas dans la sstip utilisée:
sstip white 5s[-1s[!%&x] & -1s[%]] 3 + 2
condition Circe
1.h7-h8=B 2.Bh8-b2 3.b7-b8=R 4.Rb8-a8 5.Ra8*a2[+bPa7] (x) 6.Ra2*a7 (%)
C'est ici que je ne pige pas!
|
|
|
Le problème est celui de spécificité que je viens d'évoquer (comme avec + #). Popeye donne la solution :
1.h7-h8=B 2.Bh8-b2 3.b7-b8=R 4.Rb8-a8 5.Ra8*a2 [+bPa7] 6.Ra2*a7 x
1.h7-h8=B 2.Bh8-b2 3.b7-b8=R 4.Rb8-a8 5.Ra8*a2 [+bPa7] 6.Ra2*a7 %
Elle est valide pour lui puisque Ra2*a7 réalise bien les 2 thèmes.
|
|
|
N'oublie pas que Popeye "duplique" des solutions. Donc en général il donne 3 lignes distinctes pour une solution. Dans ton problème il n'y a pas de solution, il ne donne donc que le duplicatat !
|
|
|
Prend l'exemple du problème de Jacques, la solution contient bien 3 lignes :
1.c6-c7 2.b7-b8=Q 3.Qb8-a7 4.c7-c8=Q 5.Qc8-c4 6.Qa7*a2 [+bPa7] + x
1.c6-c7 2.b7-b8=Q 3.Qb8-a7 4.c7-c8=Q 5.Qc8-c4 6.Qa7*a2 [+bPa7] +
1.c6-c7 2.b7-b8=Q 3.Qb8-a7 4.c7-c8=Q 5.Qc8-c4 6.Qc4*a2 + x
Si elle était fausse, Popeye indiquerait quand même probablement une ligne !
|
|
|
en effet, tu as raison,.
on peut d'ailleurs obtenir un petit problème correct ici avec cette même idée :
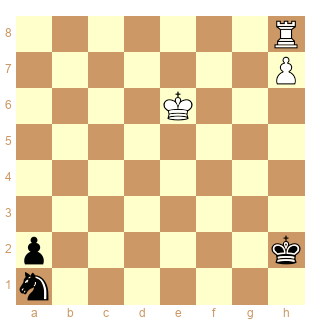
ser-%x3 "buts conjugués" Circé
Pieces
White Rh8 Ph7 Ke6
Black Pa2 Kh2 Sa1
sstip white 3s[-1s[x&!%] & -1s[%]]
condition Circe ... C+
1.Rh8-a8 2.h7-h8=B 3.Bh8*a1 [+bSb8] 4.Ra8*a2 [+bPa7] + x
1.Rh8-a8 2.h7-h8=B 3.Bh8*a1 [+bSb8] 4.Ra8*b8 %
mais il faut revoir la sstip pour qu'elle trie les fausses solutions( prise isolée avec ou sans circé ) ce n'est pas clean.
problème qui, en cas de triple but (%,x,+), ferait resurgir le "dillemme du frigidaire" avec le coup double [ 4.Ra8*a2 [+bPa7] + x ] :o)
|
|
|
Bojan a détecté depuis longtemps ce problème de doublon, d'après lui on ne peut rien y faire. Cela provient de la définition du "&" qui est cumulatif.
Même en "orthodoxe" on voit ces doublons. Notons que la sstip qui isole ce cas orthodoxe (buts A et B réalisés par le même mouvement) est simplement :
[1s[A&B]]
Schéma 19
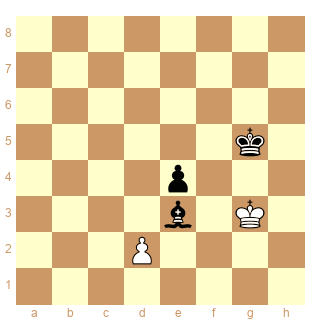
h(#&zf4)5 C+
L'output de Popeye doublone :
1.Kg5-h5 d2-d4 2.Be3-h6 d4-d5 3.e4-e3 d5-d6 4.e3-e2 d6-d7 5.e2-e1=S d7-d8=S 6.Se1-f3 Sd8-e6 7.Sf3-g5 Se6-f4 #
1.Kg5-h5 d2-d4 2.Be3-h6 d4-d5 3.e4-e3 d5-d6 4.e3-e2 d6-d7 5.e2-e1=S d7-d8=S 6.Se1-f3 Sd8-e6 7.Sf3-g5 Se6-f4 + z
Si tu arrives à modifier la sstip [1s[A&B]] pour éviter ce doublon, Dominique, je te tire mon chapeau !
Notons que je n'ai pas ajouté la condition féerique "buts multiples" dans l'énoncé, puisque ce problème est orthodoxe (il faut mater sur la case f4 par un coup unique). D'ailleurs avec l'ajout "buts multiples" c'est archi-démoli.
|
|
|
Et si les buts étaient de même nature ?
ser-+++++++++++++2 "buts conjugués", treize échecs différents (et non échec tridécuple) 2 solutions.
Les échecs doubles ne valent pas double... pour l'instant, on n'est pas en avril.
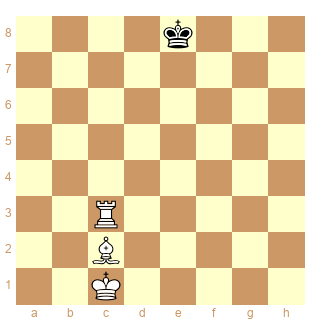
|
|
|
@ JC
Tes "Galli's" en auto-zug ne collent pas avec la théorie. En effet, c'est le coup terminal qui doit atteindre les buts, mais en auto-zug le coup terminal est celui qui donne zug, pas le suivant !
Heureusement on peut présenter tes matrices autrement, et même en mieux, en se plaçant dans le cadre des aidés inverses, qui admettent le coup terminal qui nous intéresse. J'ai trouvé la version suivante en 2 minutes (mais 2 heures pour trouver la bonne sstip !), on peut surement raffiner :
JCG version ND
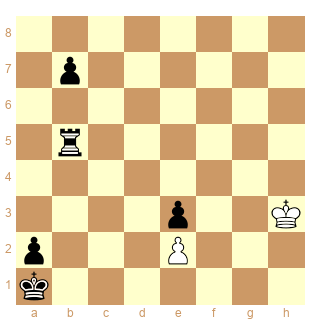
hs(#&=&+&x)5 But Associés C+
1.Kh3-g2 Rb5-b2 2.Kg2-f1 b7-b5 3.Kf1-e1 b5-b4 4.Ke1-d1 b4-b3 5.Kd1-c1 Rb2-c2 +
1.Kh3-g2 Rb5-b2 2.Kg2-f1 b7-b5 3.Kf1-e1 b5-b4 4.Ke1-d1 b4-b3 5.Kd1-c1 Rb2*e2 x
1.Kh3-g2 Rb5-b2 2.Kg2-f1 b7-b5 3.Kf1-e1 b5-b4 4.Ke1-d1 b4-b3 5.Kd1-c1 Rb2-b1 #
1.Kh3-g2 Rb5-b2 2.Kg2-f1 b7-b5 3.Kf1-e1 b5-b4 4.Ke1-d1 b4-b3 5.Kd1-c1 Rb2-d2 =
Intéressant, non ? L'aidé inverse est un genre très à la mode en ce moment, les blancs commencent et les deux camps collaborent pour que finalement les noirs n'aient pas d'autre possibilité que d'atteindre le but (les buts ici).
|
|
|
Il se passe un truc très curieux... J'ai utilisé les commandes suivantes pour vérifier le problème juste au-dessus :
begin
pieces white Kh3 Pe2 black Pa2b7e3 Ka1 Rb5
sstip white 9h [1s[+] & 1s[x] & 1s[#] & 1s[=] & !1s[!+&!x&!#&!=]]h
end
Tout va bien, sauf que si on ajoute une pièce blanche "libre", par exemple un PBg5, Popeye ne donne plus la solution attendue. Quelqu'un peut-il m'expliquer ce mystère ?
|
|
|
avec PBg5, 5...Rb2-d2 pas pat ?
|
|
|
Effectivement, merci Jacques ! J'avais l'auto-pat noir en tête... Du coup on peut retravailler la matrice pour avoir une promotion (1/4 d'AUW c'est déjà ça !). On peut encore allonger la sauce mais Popeye commence à ramer :
JCG version ND
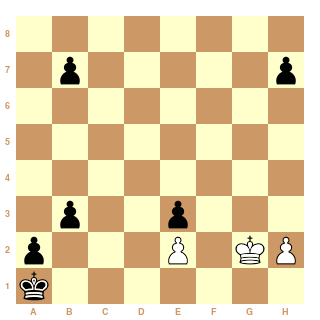
hs(#&=&+&x)7 But Associés C+
1.h2-h4 b3-b2 2.h4-h5 b2-b1=R 3.h5-h6 Rb1-b2 4.Kg2-f1 b7-b5 5.Kf1-e1 b5-b4 6.Ke1-d1 b4-b3 7.Kd1-c1
7... Rb2-c2 +
7... Rb2*e2 x
7... Rb2-b1 #
7... Rb2-d2 =
|
|
|
But = circuit (ct) : le coup terminal est un switchback.
ser-ct/ct/ct12 "buts conjugués" (Les trois buts sont de même nature. Il faut boucler les circuits aux 13es coups).
Merci de compléter l'AUW :-)
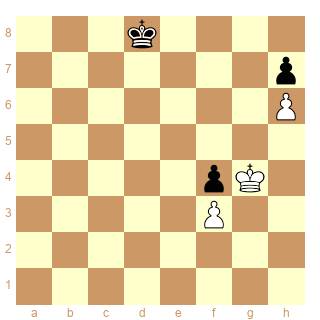
|
|
|
Notes sur le but "circuit" : un camp atteint le but si l'une quelconque de ses pièces (roi y compris) quitte la case où elle se trouve dans la position de départ et y revient en un nombre de coups quelconque, éventuellement après promotion ou renaissance.Voir ci-dessous : ser-ct4 (C+), solution 1.b8=C 2.Cc6 (2.Cd7?) 3.Cd8 4.Cb7 ct (asymétrie). Sans pion noir, démolitions par 1.R~ 2.Rb1.

|
|
|
Oui, c'est la définition que nous avons d'ailleurs retenu dans l'article sur les PJs du futur, c'est donc la bonne !
- Circuit (CI): A piece, original or promoted, leaves and returns to a given square (after any
path).
– Pawn circuit (PC): A Pawn promotes and returns to its initial square (after any path).
– Rundlauf (RU): Circuit, with the extension that the path draws a polygon of non-zero area.
– Switchback (SW): Circuit, with the extension that the path is divided into two parts, a
forward path followed by the reverse backward path.
Jacques, tu as consulté la notice de Popeye pour voir que le circuit faisait partie des buts programmés !
J'ai l'impression que ces buts sont programmés au fur et à mesure des demandes des compositeurs, on en trouve des assez exotiques (comme le circuit d'ailleurs), alors que des standards de WinChloe sont absent chez Popeye.
Par exemple "but = mouvement d'une pièce de nature donnée" n'apparait pas, ou alors j'ai mal lu ? (ça serait sympa d'avoir ce but, ne serait-ce que pour tenter de doubler le Galli's !).
|
|
|
Surtout, je suis un ancien combattant ! Phénix publiait jadis des records de longueur par matériel, pour divers buts et divers genres...
A ce propos, Problemkiste qui adore ce genre d'exercice doit paraître désormais en version web, mais je ne sais ni quand ni où.
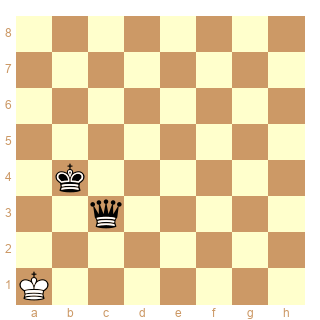
JD phénix 1992 sd-circuit-10 Sentinelles C+
1.Ra2 2.Rb1(+a2) 7.a8=T 8.Tç8 9.T×ç3 10.Ra1 Circuit
|
|
|
@ Jacques
Tu utilises quelle sstip pour plusieurs buts identiques mais non obligatoires ?
Je ne me souviens plus si Dominique l'as trouvé, je me rappelle juste de
sstip white Ns[-1s[A] & !-1s[!A]]
qui va détecter les séquences telles que chaque possiiblité de coup terminal atteigne A.
|
|
|
je pense que pour plusieurs buts identiques je traiterait comme un but obligatoire
sstip white Ns[-1s[ct] & !-1s[!ct]]
le sstip ne doit donner que les solutions réalisant le but ( impossible d'imposer un nombre de buts identique à mon avis )
la sstipp ne servant qu'à vérifier la correction du problème.
je peux me tromper mais je crois que c'est impossible autrement.
|
|
|
erratum : :o|
je "traiterais"
"un nombre donné de buts identiques"
|
|
|
En essayant ça sur le diag de Jacques l'output explose puisqu'il y a déja 6 circuits en 2 coups !
|
|
|
Oups j'avais mal lu ta proposition, Dominique.
Je ne comprends pas ton raisonnement, la sstip
white Ns[-1s[ct] & !-1s[!ct]]
ne donnera une solution que si les blancs sont obligés de terminer un circuit. Dans le diag de Jacques ça ne donne bien sûr aucune solution, puisqu'on demande juste la possibilité de terminer des circuits.
Ta as lu l'article envoyé par email ?
|
|
|
oui, cette sstip est absolument inadaptée ici, je serais curieux de connaitre l'astuce de Jacques.
Par ailleurs, j'ai bien reçu & lu ton article sur les Séries unicolores inverses. Je trouve que cette formalisation complète et légitimise le travail sur l'« auto-zugzwang » de Dan Meinking. Comme si tout un pan de séries orthodoxes trouvait sa place en pleine lumière au sein des séries plus "classiques" .
( un travail de géomètre Hamiltonien :o)
il devrait faire découvrir le genre à tous les passionnés de problèmes. J'imagine que Dan aurait beaucoup apprécié ce travail et qu'il l'aurait agrémenté d'énigmes subtiles.
|
|
|
"je serais curieux de connaitre l'astuce de Jacques."
Que son diag est "seulement" JD C+ ?
Merci pour les louanges ! J'ai du jongler entre ma volonté de faire apparaître les séries NN comme le "bon" chaînon manquant, et l'approche de Dan que je ne devais pas dévaloriser (en plus vu les circonstances tragiques...).
Dans un article en préparation, je vais partir des 4 genres de série et "remonter" aux 8 genres orthodoxes, selon que le camp qui s'intercale entre le coup initial et le coup terminal aide ou défend !
|
|
|
@ Dominique
Regarde ça stp :
Schéma 20
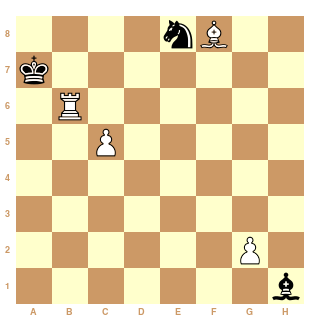
h(#&xz)2 Buts Associés
1.Cc7 Fd6 2.Ca8 Fb8 #
1.Cc7 Fd6 2.Ca8 Fc7 xz
C'est mignon je trouve car le mat seul est démoli (1.Fxg2 Fd6 2.Fa8 Fb8 #), et le cap-zug seul aussi (1.Cc7 c6 2.Ca8 c7 xz).
Mais quelle est la bonne sstip pour vérifier ça ? Le problème est que le xz n'est pas programmé comme but, donc il faut faire une sorte de "sstip imbriquée dans une autre sstip", autrement dit un joli exercice pour toi !
|
|
|
J'espère que nous sommes d'accord sur le sens de l'énoncé. Le 12 coups à trois circuits : dans la position obtenue après la série de 12 coups blancs, chacune des trois unités blanches peut (et non doit) revenir sur sa case de départ en un coup (il y a trois treizièmes coups terminaux). Le roi blanc peut aller en g4, une unité en h6... FIN DE LECTURE POUR J.-C. :o) 1.R joue (bien évidemment), 1.Rxf4 (évidemment) 2.Roi joue (bien évidemment), pas en g4 (évidemment, ni en f5), petite subtilité toutefois, puis ça roule : 7.promo... 11.promo...
L'AUW est possible ?
|
|
|
@ Jacques
C'est justement parce que j'ai bien compris l'énoncé (peut et non doit), que je me demande quelle est la sstip vérificative (i.e. pour plusieurs buts identiques facultatifs). Je préfère pouvoir contrôler si je tente un AUW.
Mais ton problème n'est pas C+, n'est-ce pas ?
@ JC
Un truc qui aurait de la gueule serait de composer un Galli-zug #z&=z&+z&xz !!!!
|
|
|
@ ND
Non, pas C+. Pour essayer de vous suivre, Dominique et toi, j'ai lu le passage sur les sstip dans la notice de Popeye, mais j'ai peu "pratiqué".
|
|
|
La difficulté est qu'une commande existe pour sélectionner les séquences telles que chaque coup terminal légal atteint le but A :
[1s[A] & !1s[!A]]
Mais on arrive pas à trouver une commande qui sélectionne les séquences telles que 4 coups terminaux atteignent A mais où il existe d'autres coups terminaux qui n'atteignent pas A.
C'est cette commande qu'il faut trouver pour tester ta demande d'un 4-circuit facultatif. Sans ça les dangers de démolition sont élevés.
|
|
|
Une bizarrerie : Les 16 travaux d'Hercule
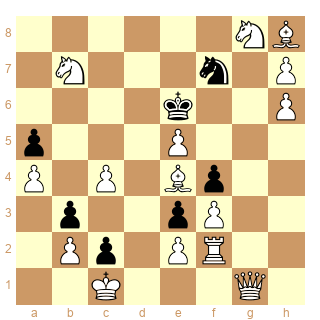
ser-d(#&+&x&=)3 Buts multiples 4 solutions
Je précise bien : buts multiples. Si un matheux veut s'amuser à compter le nombre de solutions en buts conjugués avec toutes les combinaisons possibles par cycle de buts...
PS : pour obtenir un output clean, il vaut mieux utiliser l'ancienne sstip (sans [#|+]). Sinon on a droit à des solutions incomplètes (sans le mat). Avec l'ancienne, on n'a qu'à virer les 4 + qui donnent mat et c'est impeccable. Pas de doublon, pas de chevauchement, pas de prise partagée, etc...
Je donne raison à Nico, là, pour l'intérêt qu'il y a à distinguer buts multiples et buts conjugués...
@ Jacques
Je cherche...
|
|
|
Mais, de toute façon, le problème n'est pas faux parce qu'il existe des solutions en buts conjugués.
La solution est la même jusqu'au coup terminal.
Donc il y a 4 solutions en buts multiples et, disons, 223845 en buts conjugués ;o)
|
|
|
Dans l'état actuel des définitions on n'accepte que les énoncés à Buts Associés, interdiction des énoncés en Buts Multiples, ou en Buts Conjugués. Par contre les énoncés "orthodoxes" (réalisation de plusieurs buts par le même mouvement) sont acceptés.
La raison est toujours la même, on n'a pas 2 sstips, l'une qui isole les Buts Conjugués, l'autre les Buts Multiples.
Alors tu me diras qu'on sait isoler les Buts Multiples, donc que ton problème est C+ (la solution n'est pas noyée dans l'output). C'est vrai mais je ne pense pas qu'on nous suivra si on décrète que les énoncés Buts Multiples sont autorisés, mais pas les énoncés Buts Conjugués.
Dans mon esprit ou bien on autorise les deux, ou bien on en autorise aucun, c'est logique. Si un jour on trouve la sstip manquante (celle qui isole les Buts Conjugués) on pourra autoriser les deux.
Ou alors on autorise les deux même sans sstip vérificatrice, mais alors il faut prévenir les compositeurs : vous pouvez composer en Buts Conjugués, mais en général votre travail ne pourra pas être déclaré C+ car votre solution sera noyée dans l'output, donc son unicité invérifiable. Mais je n'aime pas trop cette idée d'autoriser un genre invérifiable...
C'est un axiome de base de la théorie de la preuve : quelque chose peut être vrai sans que ça soit vérifiable, mais on ne peut pas affirmer que quelque chose est vrai sans l'avoir vérifié... C'est la distinction élémentaire qu'on fait en logique entre le "vrai" et le "prouvé". D'ailleurs un théorème célèbre affirme que dans tout système logique il existe des choses vraies mais non prouvables, on ne peut pas échapper à ça !
|
|
|
@ J.-C.
Tu peux présenter ton beau travail d'horlogerie comme un task de construction. Tu donnes la position obtenue après les trois coups de série, 4 énoncés, #1, =1, x1, +1, 4 solutions pour chacun. Et le connaisseur déguste.
Tu économises une pièce noire et même deux pions blancs.
|
|
|
@Nico
Je sais tout ça.
Ceci dit, tu aurais quand même pu te fendre d'un petit compliment;o)
Si tu savais le mal que j'ai eu à mettre en place ce truc! Avec un schéma un peu différent, j'ai passé des heures sans réussir à rétrograder un seul coup. Quand on aura trouvé la stip, ce sera un problème sympa. Et C+.
@Jacques
Merci pour ton intéressante suggestion.
Concernant ton joli dernier dernier problème, j'ai une suggestion pour l'AUW que tu sollicites et qui essaye de respecter au mieux ton schéma initial :

5 circuits en 24 coups.
Bon, c'est fait à la va-vite. Toutefois la vérification a=>b est C+.
1.Kg4*f4 2.Kf4-g3 3.f3-f4 4.f4-f5 5.f5-f6 6.f6-f7 7.f7-f8=S 8.Sf8*h7 9.Sh7-g5 10.h6-h7 11.h7-h8=B 12.Bh8*c3 13.Bc3-g7 14.c2-c4 15.c4-c5 16.c5-c6 17.c6-c7 18.c7-c8=R 19.Rc8-c6 20.Rc6*a6 21.Ra6-c6 22.a5-a6 23.a6-a7 24.a7-a8=Q a=>b
Évidemment ça n'est pas une garantie de correction, nous le savons tous.
|
|
|
Non, c'est troué. Ridicule même.
Je vais mieux y réfléchir.
|
|
|
@ JC
Je n'ai hélas pas le temps ni de composer ni de solutionner, m'occupant exclusivement de mettre au point la théorie, et il y a du boulot !
Donc je n'ai pas analysé ta position (je te félicite quand même !), me contentant de remarquer qu'elle crée des dégats théoriques, qu'on décide de l'accepter ou de la rejeter !
Pour résumer le dilemne que je n'arrive pas à trancher :
- Ou bien on met tout dans le même sac "Buts associés", et ton problème au-dessus est démoli.
- Ou bien on sépare les sacs, alors ton problème au-dessus est C+, mais le sac "Buts conjugués" est invérifiable en général.
En fait il manque 2 sstips, celle pour les buts identiques facultatifs, et celle qui isole les buts conjugués. Je commence à penser que non seulement elles n'existent pas pour le moment, mais qu'en plus elles sont impossibles à programmer.
|
|
|
Nico, ce que j'essayais de prouver, entre autres, avec le problème ci-dessus, c'est que les choses sont peut-être encore plus compliquées.
Étant donné que les 3 coups de série qui précédent les coups terminaux sont, dans tous les cas, identiques, je peux présenter cette composition en "buts associés" en précisant qu'elle comporte n solutions (les 16 prévues en "buts multiples" ajoutées aux je ne sais pas combien en "buts conjugués" -mais c'est un nombre fini-).
Dès lors on ne peut plus parler de démolition au sens strict, non?
Je ne sais pas si tu comprends ce que je veux dire.
|
|
|
je pense que le sac "Buts conjugués" est programmable, mais par fonctions; dans Popeye ou Winchloé, mais les sstip de Popeyes montrent ici leurs limites. Impossible de d’associer un but à un type de pièce par exemple.
pour le schéma 20 c'est peut être encore possible... mais je n'ai pas trouvé:) c'est pourtant assez proche d'un "simple" !zx en rex inclusif non? ... impossible de trouver la sstip qui donne les deux réponses attendues ( en fait j'ai ces réponses , mais parasitées de démolitions.
trouver une solution forcée !! ok... c'est dans les cordes des stipp
trouver une solution aidée ?! c'est plus délicat... mais c'est à la portée du programmeur bien sûr. ( sans doute au prix de la multiplication des buts ici )
par ailleurs je suis impressionné par les problèmes de Jean Christian aux multiples buts et AUW! J.C.: pour Chess Jewelry sans doute !
Il va falloir ici des stipp en plusieurs volumes ^.^ ... mais cela me parait compromis. ( à mon grand regret :)
|
|
|
@ Jacques
Quel est le task sur les circuits, exactement ? 4 pions promus en AUW achèvent chacun un circuit de pion au coup terminal, sachant que l'énoncé stipule que 4 circuits de pion ont été effectués ?
Car ta solution est surement :
1.Rxf4 2.Rg3 7.f8=C 8.Cxh7 9.Cg5 10.h7 11.h8=F 12.Fg7 13.Cf3 Fh6 Rg4.
Donc on parle bien de circuit de pion et pas de circuit en général ? Sinon tu pourrais terminer par exemple par Fh8->a1->h8 = circuit.
|
|
|
Merci, Dominique ;o)
Une question, à Jacques notamment : est-ce que, dans un circuit, un pion promu qui revient (sous forme de pièce bien sûr) sur sa case de départ a le droit de le faire en donnant échec au roi adverse?
|
|
|
@ JC
Oui je comprends ce que tu veux dire.
La condition "buts associés" signifie que l'oeuvre est soit un "buts conjugués", soit un "buts multiples", mais pas les deux en même temps !
Donc même si ton problème était aussi C+ en "buts conjugués", il serait C- en "buts associés".
D'ailleurs il a bien été stipulé plus haut "premier arrivé, premier servi", et si une solution conjuguée arrive en même temps qu'une solution multiple, c'est démoli en associés (c'est parfaitement logique, tes petits-enfants sont des garçons ou des filles, s'ils sont les deux en même temps, leurs chromosomes sont défectueux !).
Croisement, je crois pouvoir répondre à ton autre question aussi : je ne vois rien qui empêche un coup terminal de donner échec, même en achevant un circuit de Pion.
|
|
|
Je viens de vérifier avec Popeye :
- Un circuit débutant par un coup de Pion est toujours considéré comme un circuit de Pion (un circuit de la figure promue ne compte pas).
- L'échec terminal est autorisé.
|
|
|
@ Dominique
Je prépare un petit résumé pour le fil suivant. Est-ce que tu peux me dire si tout est correct et si je n'ai rien oublié ? Merci à l'avance.
Soient A et B deux buts distincts, aucun n'étant inclus dans l'autre.
1) Buts orthodoxes : les 2 buts sont atteint par le même mouvement.
a) [1s[A & B]] isole ce cas en facultatif.
b) [1d[A & B]] isole ce cas en obligatoire.
2) Buts multiples : les 2 buts sont atteint par des mouvements différents de la même pièce.
a) Pas de sstip isolante en facultatif.
b) [1s[A&B] & !1s[A&!B] & !1s[B&!A]] isole ce cas et l’orthodoxe en obligatoire.
3) Buts conjugués : les 2 buts sont atteint par des mouvements de pièces différentes.
a) Pas de sstip isolante en facultatif.
b) Pas de sstip isolante en obligatoire.
4) Buts associés : les 2 buts sont atteint par l'une des possibilités précédentes.
a)[1s[A] & 1s[B] | !1s[!A|!B]] isole ce cas en facultatif.
b) [1s[A] & 1s[B] & !1s[!A&!B]] isole ce cas en obligatoire.
|
|
|
Pour l'AUW circuit de Jacques, difficile de discriminer entre promotion en dame, en tour et en fou de cases blanches. Mais on doit pouvoir y arriver.
Peut-être ça?

ser-ct/ct/ct/ct/ct 23 Buts associés (5 circuits à boucler)
1.Kg4*f4 2.Kf4-g3 3.f3-f4 4.f4-f5 5.f5-f6 6.f6-f7 7.f7-f8=S 8.Sf8*h7 9.Sh7-g5 10.h6-h7 11.h7-h8=B 12.Bh8*d4 13.Bd4-g7 14.d3-d4 15.d4*c5 16.c5-c6 17.c6-c7 18.c7-c8=Q 19.Qc8*a6 20.Qa6-g6 21.a5-a6 22.a6-a7 23.a7-a8=R a=>b
Puis bouclage avec 24.Kg4/Sf3/Bh6/Qd3/Ra5
|
|
|
Bon, puisque je n'arrive pas à me décider avec le seul recours de la théorie, j'ai examiné le problème sous l'angle de la pratique.
Il apparait que le "buts conjugués" est souvent mangé par le "buts multiples", comme c'est le cas dans quelques tests que j'ai pu faire, il est en général plus facile d'atteindre 2 buts par 2 mouvements de la même pièce, que par des pièces différentes.
De plus, manque de bol, le "buts conjugués" est justement celui pour lequel on n'a pas de sstip isolante.
Mais si on n'autorise pas le "buts conjugués" tout seul, on va perdre plein de possibilités de travaux intéressants, qui seront noyés dans des "solutions" en buts multiples.
Donc finalement, je reviens à mon sentiment premier, on a intérêt à dissocier les genres, même si on n'a pas toutes les sstip correspondantes. Mieux vaut avoir des genres "petits" qu'on peut associer si on veut, que des genres "grands" qu'on a pas le droit de dissocier...
|
|
|
Ca a une belle tête de vainqueur ton histoire JC...
Si oui c'est un très joli problème, chouette thème et chouette présentation. Et placement judicieux du Roi Noir !
Tu n'as plus qu'à prier pour que Bojan ou Dominique trouve la sstip en buts identiques facultatifs, sinon tu auras toujours une épée de Damoclès au-dessus de ton problème...
C'est pour ça que je n'aime pas beaucoup composer sans vérification possible. Quand tu vois le nombre de problèmes de nos glorieux
ancêtres qui sont maintenant démolis, ça fait peur...
|
|
|
Message de Bojan :
- Pourquoi pas simplement [1s[A] & 1s[B]] à la place de [1s[A] & 1s[B] | !1s[!A|!B]] ?
- Impossible de stipuler pour le moment le conjugué seul, mais une programmation spécifique est envisageable.
- Pas de solution évidente pour un multiple but identique A en facultatif, mais pas d'abandon de recherche pour le moment.
Vraiment sympa ce Bojan, va falloir lui dédier quelque chose. Pourquoi pas ton problème au-dessus JC, s'il arrive à trouver la bonne sstip pour le vérifier ?
|
|
|
le résumé me convient parfaitement... il clarifie même la situation dans mon esprit :o)
« Soient A et B deux buts distincts, aucun n'étant inclus dans l'autre. » oui je pense qu’il faut verrouiller ici aussi dès lors que l’on peut dissocier clairement les buts tout ce que nous avons produit ici fonctionne. Pour les autres buts, disont « jointifs », il faut sans cesse faire des aménagements qui peuvent donner des effets de bords à nos sstip.
concernant le
2) Buts multiples : les 2 buts sont atteints par des mouvements différents de la même pièce.
a) sstip isolante en facultatif. : ce pourrait bien être [ 1s[A] & 1s[B] & !1s[A&B]] en effet !1s[A&B]] ôtes tous les buts multiples atteints par une même pièce ( par construction.
)
[1s[A] & 1s[B]] seul ne suffit pas car il laisse tous les coups multiples ... absolument tous !
Reconsidérons le schéma 14 si rebelle aux Buts conjugués:

Recherchons les coups multiples en reprenant pas à pas les output de Popeye.
Etape 1 : sstip black 1s[ 1s[+&x]]
1.Ka6-a7 Bd2-e3 + N.B. ici il n’affiche pas Bd2*f4 x …le +, premier nommé est prioritaire ?
Etape 2: sstip black 1s[ 1s[x&+]]
1.Ka6-a7 Bd2*f4 x N.B. ici il n’affiche pas Bd2-e3 + …le x, premier nommé est prioritaire ?
Etape 3 : sstip black 1s[ 1s[+] & 1s[x]]
1.Ka6-a7 Bd2-e3 +
1.Ka6-a7 Bd2*f4 x N.B. la première réponse en multiple est complète
C’est ici qu’il faut garder son attention !
Etape 4 : sstip black 2s[ 1s[+] & 1s[x]] ( en deux coups !)
1.Ka6-a7 Bd2-e3 +
1.Ka6-a7 Bd2*f4 x
1.Ka6-a7 2.Ka7-b8 Bd2*f4 + x N.B. nous retrouvons tous les multiples ..
Etape 5 : sstip black 2s[ 1s[+] & 1s[x] & 1s[+&x]]
1.Ka6-a7 2.Ka7-b8 Bd2*f4 + x N.B. la première réponse en multiple par une même pièce… seule
Etape 6 :
sstip black 2s[ 1s[+] & 1s[x] & !1s[+&x] ]
1.Ka6-a7 Bd2-e3 +
1.Ka6-a7 Bd2*f4 x N.B. bien qu'en deux coups..les multiples par une même pièces ont disparu
2) Buts multiples : les 2 buts sont atteints par des mouvements différents de la même pièce.
la sstip isolante en facultatif pour les Buts multiples est donc :
[ 1s[A] & 1s[B] & !1s[A&B]]
|
|
|
toujours avec ce schéma 14.
il révèle l'impossibilité de trouver une stipp pour les Buts conjugués ( version actuelle)
Buts conjugués : les 2 buts sont atteint par des mouvements de pièces différentes.
1.Ka6-a7 2.Ka7-b8 3.Kb8-c8 4.Kc8-d8 5.Kd8-e7 6.Ke7-f6 7.Kf6-f5 8.Kf5-g5 (8...h2-h4 + ;8...Bd2xf4x+)
il faut :
a)soit que le programmeur implémente une fonction Buts conjugués ( version complexe et peut être but par but (?)
b)soit qu'il crée un opérateur ( comme & ou | ...) qui permette d'inclure dans une sstip cette restriction :"pièces différentes."
c'est la seconde implémentation qui aurait pour moi la préférence, car elle resterait un outil universel pour le programme et donc une liberté de lui découvrir des utilisations futures, peut être sans lien avec le fil actuel.
notons par exemple "§" cet opérateur discriminant la pièce et le but:
A§B : les buts A & B sont atteints par des "pièces différentes."
Comme !A|!B signifie !(A&B) alors !1s[!A|!B] devrait s’écrire !1s[!(A§B)]
nous pourrions, grâce à cet opérateur §, peut être avoir maintenant les deux sstip manquantes de la manière suivantes :
3) Buts conjugués : les 2 buts sont atteint par des mouvements de pièces différentes.
a)[1s[A] & 1s[B] | !1s[!(A§B)] isole ce cas en facultatif.
b) [1s[A] & 1s[B] & !1s[!A§!B]] isole ce cas en obligatoire.
|
|
|
@ Dominique
Peux-tu indiquer stp, la différence entre [1s[A] & 1s[B]] et [1s[A] & 1s[B] | !1s[!A|!B]] ? (question de Bojan)
"la sstip isolante en facultatif pour les Buts multiples est donc : [ 1s[A] & 1s[B] & !1s[A&B]]"
Tu es sûr que les buts conjugués sont bien enlevés ? Parce que si Bojan a raison, donc que [1s[A] & 1s[B]] code le but associé, tu ne fais que retirer le but orthodoxe, donc il reste effectivement le but multiple, mais aussi le but conjugué (souvent noyé loin dans l'output, comme pour le schéma 14, construit exprès).
|
|
|
erratum :
b) [1s[A] & 1s[B] & 1s[A§B]]isole ce cas en obligatoire.
Schema 14-bis
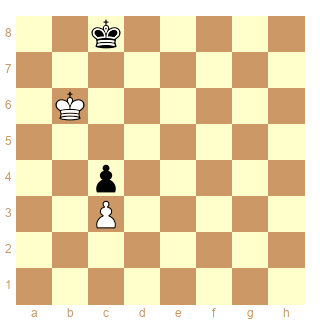
Pieces
White Kc6 Pd3 Ph2 Ba1
Black Kc8 Pd4
sstip black 4s[ 1s[+] & 1s[x] & !1s[+&x]]
isole deux solutions l’une à buts conjugués l’autre à buts multiples que nous pouvons séparer avec notre nouvel opérateur § par
1s[A§B] ou !1s[A§B] selon que nious désirons la solution par mouvement d’une même pièce ( n’atteignant pas les deux buts en un même coup ) ou la solution par mouvement de deux pièces différentes.
[1s[A] & 1s[B] & !1s[A&B]] & 1s[A§B]]
devrait isoler la solution suivante :
1.Kc8-d8 2.Kd8-e7 3.Ke7-f6 4.Kf6-g5 ( 4...h2-h4 + ;4...Ba1*d4 x ) solution unique pour buts conjugués
[1s[A] & 1s[B] & !1s[A&B]] & !1s[A§B]]
devrait isoler la solution suivante :
1.Kc8-b8 2.Kb8-a7 3.Ka7-a6 4.Ka6-a5 ( 4...Ba1-c3 + ;4...Ba1*d4 x ) solution unique pour buts multiples
croisement : tu as entièrement raison: [ 1s[A] & 1s[B] & !1s[A&B]] garde bien le but multiple & le but conjugué ! là où j'en suis je dirais qu'il faut reprogrammer Popeye pour aller plus loin.
il me semble que celà pourrait marcher avec l'opérateur § ci dessus.
|
|
|
@ JC
J'ai essayé de prolonger le hs(#&=&+&x)7 But Associés C+ du 08/03/2013 - 11:12:37.
En fait c'est un buts multiples et Popeye trouve des démolitions incroyables après prolongation. Son plan est de pater le Roi blanc avec une Dame. Comme ça le Roi noir est libre, chacun de ses coups étant un pat (inactif). Il s'arrange ensuite pour que chaque mouvement de la Dame patente soit un échec, un mat ou une capture, et c'est démoli !
Trop malin ce Popeye...
|
|
|
oui ce lièvre avait été levé avec le fameux pion h4 de J.C dès que Popeye trouve une position de pat il ne puis reste qu'a y associer #,x+ et tout est démoli!
le défit de J.C n'en est que plus difficile! Il faut éviter toute possibilité de "pat prématuré"! boujour le task.
|
|
|
Bojan a raison :
la différence entre [1s[A] & 1s[B]] et [1s[A] & 1s[B] | !1s[!A|!B]] n'existe pas . en fait les test sont redondants.
|
|
|
@ Dominique
"dès que Popeye trouve une position de pat il ne reste qu'a y associer #,x+ et tout est démoli!"
Oui c'est exactement ça !
Il me reste une dernière question pour mon résumé à venir. Quelle est la généralisation à 3 buts de la sstip :
[1s[A&B] & !1s[A&!B] & !1s[B&!A]]
Est-ce bien :
[1s[A&B&C] & !1s[A&!B&!C] & !1s[B&!A&!C] & !1s[C&!A&!B]] ?
|
|
|
ma première impression est que !1s[A&!B&!C] ne suffit pas :
[A&!B&!C] : Avoir (A et ni B ni C) est juste mais il manque (A et B et nonC) et (A et C et non B)
[A&!B&!C] devrait être remplacé par : [A&B&!C]&[A&C&!B]&[A&!B&!C]
jecrois que la généralisation est plutôt:
[1s[A&B&C] & !1s[A & !(B|C) & !1s[B & !(C|A)] & !1s[C & !(A|B)]]
|
|
|
Oops ! ( encore) il me semble que j'ai écrit la même formulation que toi !
la bonne généralisation est:
[1s[A&B&C] & !1s[A & !(B&C)] & !1s[B & !(C&A)] & !1s[C & !(A&B)]]
que l'on peut écrire aussi :
[1s[A&B&C] & !1s[A & !(!B|!C) & !1s[B & !(!C|!A)] & !1s[C & !(!A|!B)]] mais je préfère la précédente plus lisible.
|
|
|
Merci. Je vais maintenant pouvoir envoyer un résumé qui servira d'introduction à une nouvelle guirlande. Celle-ci s'achève bientôt, pas de repos pour les braves compositeurs !
|
|
|
Juste un mot en passant :
Vous faites tous les deux un excellent boulot, fastidieux mais nécessaire, en passant en revue toutes ces sstip déroutantes et en essayant de les trier et de les classifier. Trop nul pour vous aider dans ce domaine. Courage, donc!
Nico, tu me demandes de dédier à Bojan la version AUW du problème à circuits de Jacques. Moi je veux bien, mais ce problème ne m'appartient pas. Jacques est l'initiateur du thème, du schéma pour les 2 premières promotions (j'en reprends les 11 premiers coups) et de l'idée de rechercher l'AUW.
Je me sens donc à peine autorisé à cosigner cette version AUW, si Jacques le veut bien.
Dans tous les cas son accord est nécessaire pour la dédicace à Bojan.
D'autre part ne perdons pas de vue que le problème n'est pas (encore?) C+.
Mais plus je le regarde, plus il me semble correct, tant les contraintes sont lourdes en termes d'ordre et de nature des promotions, et de positionnement de la pièce promue pour le retour à la case départ.
|
|
|
Vous travaillez vraiment bien quand je me repose !
L'AUW à 5 circuits est très réussi, merci J.-C. Et correct de toute évidence. Tout à fait d'accord pour la co-signature et la dédicace.
@ N. D. : WinChloe traite le but "mat sur telle case". Ton aidé 7 coups (mat sur f4) est C+/Chloé. Dans la base Echecs, on trouve seulement 10 problèmes directs des 16e et 19e siècles.
|
|
|
Un problème passé inaperçu (publié ci-dessus) ? Je suis content que le coup terminal soit compté (voir fil "Buts Associés pour les Pros").
Le "nouvel" énoncé est ser-(+,+,+,+,+,+,+,+,+,+,+,+,+)3, Buts Associés, 2 solutions. 13 coups terminaux donnant échec.
Début avril, ce serait 15 ;o))

1.Fe4 2.Te3 3.F~+
1.Tc6 2.Fa4 3.T~+
|
|
|
Oui je n'ai pas bien compris pourquoi parfois un énoncé était pré-terminal. On n'est pas en zug. D'ailleurs même en zug il existe un coup terminal, celui qui atteint le but Az (voir la reprise par Dominique, dans le nouveau fil, d'un schéma qui illustre ça). C'est pour cette raison que dans l'article je parle de "coup virtuel" pour désigner un coup post-zug, et non pas de "coup terminal".
|
|
|



