|
| Rétro Colorier les pièces par zoug le
[Aller à la fin] |
| Problèmes | |
Dans Winchloé, quelles conditions faut il imposer dans le filtre ou les requêtes pour obtenir les problèmes du type Colorier les pièces
|
|
|
Requête -> Extension de l'énoncé like %olori%
"olori" permet d'avoir les énoncés avec "colorier", "Colorier" ou "coloriage".
On a 143 problèmes dans la base de WInchloé. Curiosité : Kornilov et Frolkine ont chacun composé plus de la moitié des ces problèmes ! (évidemment un problème peut avoir plusieurs auteurs).
Le suivant dans la liste est bien connu ici, c'est Alain Brobecker (mais 6 problèmes seulement dans la base, il en a composé beaucoup plus je crois).
|
|
|
Un exemple simple, de Pascal Wassong (Phénix 1998)
Colorier les pièces (sous-entendu : pour obtenir une position légale)
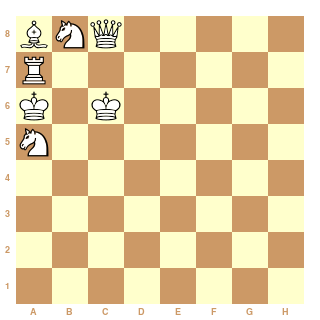
|
|
|
simple ...?
autant je proposerais Ra6 et Ta7 noirs avec comme dernier coup : -1 : b7-b8C+
autant je ne vois pas le coup -2
|
|
|
Donc c'est Ra6 et Ta7 blancs avec -1. c7xb8C+ ?
|
|
|
le Ra6 serait en échec avec la Dç8...
|
|
|
Dame blanche, of course.
|
|
|
ok
merci
|
|
|
Aviez-vous pensé à cela, avec b7-b8C+ comme dernier coup ?
BNQ5/r7/k1K5/N7/8/8/8/8
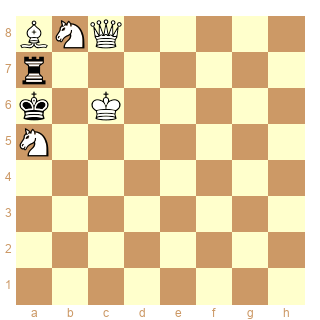
|
|
|
quel aurait été le dernier coup noir ?
(19:57:02)
|
|
|
Incidemment, je vous rappelle qu'un problème de coloriage, plus trapu que celui de Pascal, vous attend ici.
Tic tac, tic tac...
|
|
|
Bravo Orouet. C'était l'"essai thématique".
|
|
|
François, pour Winchloé je ne sais pas, mais sur la chess problem database (http://www.softdecc.com/pdb/index.pdb) il suffit de taper K='coloring problem'...
228 problemes
|
|
|
Merci Alain;je viens de demander un mot de passe à cette base et irai la consulter de temps en temps.J'ai déja travaillé sur certains de tes problèmes du type Colorier les pièces.C'est un genre très attractif
|
|
|
Avant b7-b8 C+ quel est le coup des Noirs ? Peut être^est il évident !
|
|
|
@Zoug
juste ! il est impossible de trouver un coup noir précédent.
d'où la solution correcte de Bellamy.
|
|
|
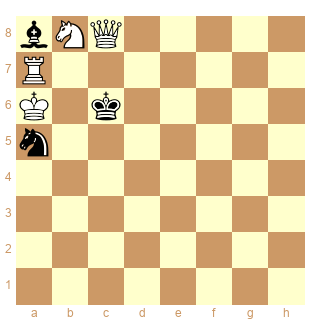
A savoir
bNQ5/R7/K1k5/n7/8/8/8/8
Comme quoi on n'est jamais assez clair...
Bravo Bellamy, Orouet... et Pascal.
|
|
|
A présent, mon estime pour Orouet (et Bellamy) doublera s'ils s'attaquent à celle que j'ai mise en lien. Mon estime pour Pascal ne changera pas puisque 1) il la connaît 2) il est capable, même sans la connaître, de la résoudre en 10 mn.
|
|
|



