|
| Des cavaliers qui rendent fou par ins7708 le
[Aller à la fin] |
| Problèmes | |
J'étais tombé par hasard sur le petit exercice suivant :
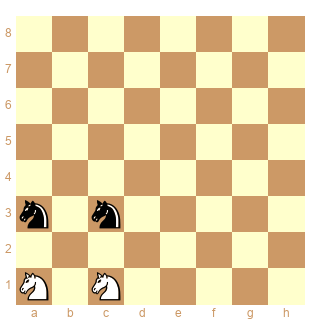
Sans quitter le carré défini par la diagonale a1-c3, en combien de coups peut on inverser les cavaliers blancs et noirs ?
Ca m'a quelque peu inspiré :
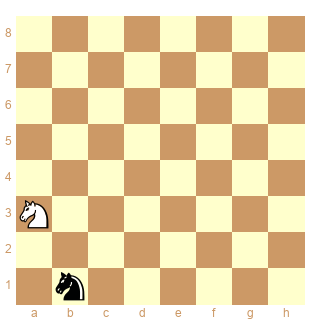
Même énoncé.
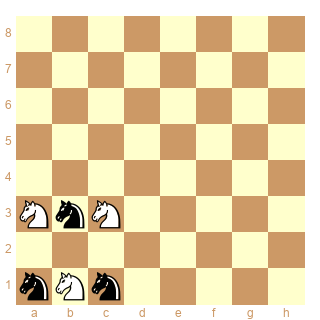
Même énoncé.
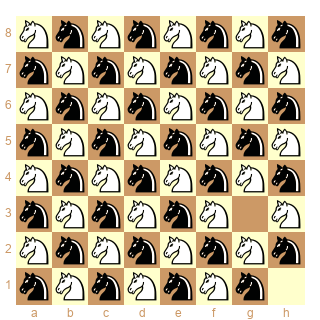
Et sur l'ensemble de l'échiquier :
en combien de coups minimum peut-on inverser les cavaliers blancs et noirs ?
Et enfin, c'est une vraie question car je ne suis pas certain de moi : pour le suivant j'ai une solution en 992 coups, est-ce bien le minimum ?

|
|
|
Ah tiens, un des diagrammes n'est pas passé. C'est le facile des deux sur l'ensemble de l'échiquier. En combien de coups minimum peut-on inverser cavaliers blancs et noirs ?
Reyes, le code img fonctionne en preview mais pas l'article une fois validé ? (normalement je ne l'utilise pas, mais là il n'y avait pas de cas où j'utilisais diag...)
|
|
|
10-4-10. Après ?
|
|
|
Je cherche le schéma récursif qui permet de ne pas devenir fou
|
|
|
Hum... non, non et non...
Sinon, celui que j'ai reposté est trouvable et il y a effectivement une astuce qui, une fois trouvée, permet de le résoudre en quelques secondes.
|
|
|
Enfin pour trouver l'astuce, il vaut mieux avoir entendu parler du problème du cavalier (Al-Adli puis Euler). En l'occurrence, savoir que un cavalier peut faire le tour de l'échiquier en visitant une seule fois chaque case.
|
|
|
Pour le tout premier, la solution est en 16 demi-coups. Voir ici
|
|
|
Dans "Mathématiques pour le plaisir" de Jean Paul Delahaye il y a
un court paragraphe avec le problème suivant ci-dessous, et un
rappel de la méthode pour résoudre ces problèmes
(changement de plateau et les cavaliers deviennent des "rois orthogonaux").
Les cases avec un PN sont interdites.
Il faut 44 mouvements pour procéder à l'échange.
Je peux envoyer le court article par mail: abrobecker_a_yahoo_point_com
|
|
|
Pardon, 40 coups.
44 c'est lorsque les CB sont en a1 et c3
|
|
|
J'ai d'abord cherché une solution en alternant coup blanc et noir (dans mes problèmes il faut le faire). J'ai mis du temps à comprendre qu'il ne fallait évidemment pas (nombre impair de coups pour chaque camp) Voici une solution.
1. N4c3 -- 2. Nb1 -- 3. Na3 -- 4. Nc2 Na4 5. -- Nc3 6. -- Nb1 7. -- Na3 8. --
Nb2 9. -- Na4 10. -- Nc3 11. -- Ncb1 12. Nc3 -- 13. Na4 -- 14. Nb2 -- 15. Nd3
Nc3 16. -- Na4 17. -- Nb2 18. -- Nb1 19. -- Nc3 20. -- Nca4 21. Na3 -- 22. Nb1
-- 23. Nc3 -- 24. Na2 Nc3 25. -- Nb1 26. -- Na3 27. -- Na4 28. -- Nc3 29. --
Ncb1 30. Nc3 -- 31. Na4 -- 32. Nab2 Nc3 33. -- Na4 34. -- Nb1 35. -- Nbc3 36.
-- Na2
Je connais pas la méthode du changement de plateau des rois orthogonaux et pour être franc j'ai rien compris à ce que ça signifie, mais j'ai un moyen visuel assez simple qui permet de résoudre ces problèmes à l'aveugle.
D'ailleurs, j'ai pas compris l'intérêt de laisser la case b3 libre....
|
|
|
Euh, je crois bien qu' on peut alterner coups blancs et noirs...
|
|
|
Et qu' on doit !
|
|
|
Non, non et non? Exact. Je viens de relire l'énoncé, mais c'est trop tard. Les cavaliers m'ont déjà rendu fou..... temps de plier l'échiquier et de partir en vacances.
Merci pour le "puzzle" de l'été.
|
|
|
"Euh, je crois bien qu' on peut alterner coups blancs et noirs... "
Heu, si la solution dure 40 demi coups et qu'on alterne, ça fait 20 demi coups chacun.
Or les cavaliers blancs sont sur la même couleur et les cavalier noirs sur couleurs opposées.
Donc pour s'inverser, les deux camps doivent forcément jouer un nombre de coups impair.
On ne peut pas alterner, CQFD.
Me trompé-je ?
|
|
|
Non tu ne te trompes pas, ça doit être le nombre de coups qui n'est pas bon (repris depuis l' article).
Je regarde plus précisément cet après-midi.
|
|
|
Ma méthode pour les 3*3 :
Chacune des cases est reliée à deux autres. On peut considérer qu'elles forment un cercle (enfin ici représenté par un segment)
a1-b3-c1-a2-c3-b1-a3-c2
Là dessus, on peut se déplacer d'une case à gauche ou d'une case à droite. Et quand on arrive en c2, on peut revenir directement en a1.
Par exemple pour le problème avec un cavalier chacun, l'un en a3 l'autre en b1, on comprend tout de suite qu'un des cavaliers doit faire tout le tour, par exemple Ca3-c2-b1-a1-b3-c1-a2-c3-b1 soit 7 coups.
Pour le problème de Dalahaye, il suffit d'écrire
d3-b2-a4-c3(a2)-b1-a3-c2-a1-b3
Ici il s'agit bien d'un segment et non d'un cercle car d3 et b3 ne sont évidemment pas reliées.
La case (a2) sert uniquement de cage pour faire coulisser les cavaliers.
Au début on a les deux noirs à tout à gauche du segment : d3 et b2, un cavalier blanc dans la cage a2, l'autre en a4.
Il suffit donc de faire passer le Ca4 vers la droite jusqu'en c2, puis les deux cavaliers noirs jusqu'en b1 et a3. Ca permet de mettre le cavalier a2 tout à gauche en d3. Puis on refait passer les cavaliers noirs à gauche de la cage en b2 et a4. Ainsi on peut mettre le cavalier blanc dans la cage en a2. Puis faire passer les cavaliers noirs à droite en b1 et a3. Et c'est fini : le cavalier a2 rejoint b2 et les cavaliers noirs respectivement a4 et a2.
Evidemment cette méthode ne marche que lorsque chaque case est reliée à deux autres (et ici une seule à trois autres).
Pour le problème aux 62 cavaliers, il faut être un peu plus malin, mais la solution (qui est juste le nombre de coups, pas de les jouer) se résume à une addition élémentaire.
|
|
|
Petiteglise tu as raison, il y a bien un blocage si on essaye d'alterner coups blancs et noirs dans le problème de Delahaye...
Preuve que je ne l' avais jamais vraiment cherché jusqu'à aujourd'hui.
Par roi orthogonal j'entendais un roi qui ne peut pas aller en diagonale et qui n'a plus sa particularité royale. J'aurais pu dire une tour qui ne bouge que d'une case. Ou aussi bondisseur (1 ; 0).
|
|
|
Oui ok, ça équivaut à la méthode que j'ai expliquée plus haut.
Personne n'a d'idée pour les 62 cavaliers ? (celui que j'ai reposté en dessous de l'article).
|
|
|
Pour le problème de Delahaye, tu dessines tes 9 cases d3-b2-a4-c3-b1-a3-c2-a1-b3 cote à cote, tu place une case a2 au dessus de c3, tu places des "rois orthogonaux" sur a2 ; a4 ; b2 ; d3 et tu as un problème équivalent à celui avec les cavaliers.
C'est à peu de choses près la même idée que la tienne.
Yapuka corriger/ modifier le Delahaye.
|
|
|
Croisement
|
|
|
Pour 62 cavaliers, il y a au moins 2+62 coups.
|
|
|
64 demi coups n'est pas la réponse.
|
|
|
Hummm, on pourrait chercher les circuits (Eulerien ? ) de cavaliers dans lequel les cases vides sont les plus "proches" ?
Mais je crois qu'il y a beaucoup de ces circuits ?
|
|
|
62+3 après réflexion. C'est un minorant, pas la réponse que tu attends.
|
|
|
Oui comme j'ai écrit à 10h28, ça rejoint Euler / Al-Adli.
Comme il y a un nombre pair de coups, tu peux minorer plus haut encore.
|
|
|
Solution :
on sait (depuis le IXème siècle) qu'il est possible de faire un tour de l'échiquier à un cavalier en passant une fois par chaque case, jusqu'à ce qu'il revienne à sa case de départ (64 coups = 64 cases).
Comme le circuit est fermé, on peut le commencer par n'importe quelle case. En outre, il passe forcément par h1, accessible par g3 et f2.
On comprend qu'il est donc possible de commencer un tel tour par f2 (case 1) et de le finir par h1 (case 64) avec pour avant dernière case g3 (case 63).
Les cavaliers blancs occupent donc toutes les cases paires de ce circuit de 2 à 62 et les cavaliers noirs les cases impaires de 1 à 61.
Au premier coup on joue le C sur la case 62 sur la case 63 (g3).
Au deuxième coup on joue le C sur la case 61 sur la case 62.
Au troisième coup on joue le C sur la case 60 sur la case 61
etc.
Au bout de 62 demi coups soit 31 coups, tous les cavaliers ont changé de place, sauf le blanc en g3 qui devrait se trouver en f2.
Ca lui prend 2 coups, durant lesquels les noirs patientent en jouant C62 en 63 puis C63 en 62.
Au total on a donc 33 coups soit 66 demi coups.
C'est évidemment le minimum.
CQFD.
|
|
|
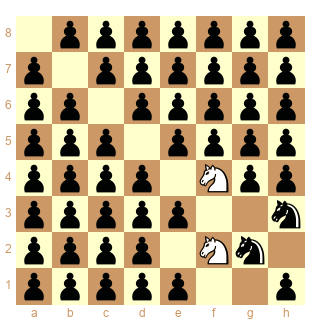
Pour le troisième diagramme il n'y a que 2 solutions (une seule à symétrie près), en 12.0 coups :
1.Sc1-a2 Sa3-c2 2.Sb3-c1 Sb1-a3 3.Sa1-b3 Sc3-b1 4.Sa2-c3 Sc2-a1 5.Sc1-a2 Sa3-c2 6.Sb3-c1 Sb1-a3 7.Sc3-b1 Sa1-b3
8.Sa2-c3 Sc2-a1 9.Sc1-a2 Sa3-c2 10.Sb1-a3 Sb3-c1 11.Sc3-b1 Sa1-b3 12.Sa2-c3 Sc2-a1 a=>b
1.Sa1-c2 Sc3-a2 2.Sb3-a1 Sb1-c3 3.Sc1-b3 Sa3-b1 4.Sc2-a3 Sa2-c1 5.Sa1-c2 Sc3-a2 6.Sb3-a1 Sb1-c3 7.Sa3-b1 Sc1-b3
8.Sc2-a3 Sa2-c1 9.Sa1-c2 Sc3-a2 10.Sb1-c3 Sb3-a1 11.Sa3-b1 Sc1-b3 12.Sc2-a3 Sa2-c1 a=>b
Evidemment c'est Popeye qui a fait le job, en utilisant un échiquier non-standard et la commande dia a=>b pour passer d'un diagramme à l'autre.
|
|
|
Je suis tombé sur cette présentation hier soir Mickael Launay et les cavaliers d'Al Adli (qui reprend la méthode mentionnée par Petiteglise)
Présentation des problèmes
http://www.youtube.com/watch?v=YfI7iQrqKGg
Solution
http://www.youtube.com/watch?v=HcUvd-v6x0o
|
|
|
Les explications sont limpides même si beaucoup trop longuettes à mon goût.
Je trouve regrettable son choix de présenter une inversion en 8 demi coups au lieu de 14 dans le cas 1C vs 1C et 8 demi coups au lieu de 24 dans le cas 3C vs 3C. Mais c'est peut-être pour simplifier.
Et il ne fait pas jouer un coup chacun, ce qui est un peu bizarre même si pas important dans ce cas.
Nombre de vues assez impressionnant vu le sujet. La prochaine fois que je compose un problème "d'échecs et maths", je le posterai sur Youtube, pas sur FE :)
|
|
|
Vous connaissez le dernier problème du type "le dernier coup détermine entièrement la partie" ?
Il s'agit de trouver la partie qui se termine par 7...Rxb7# (Alex Fishbein, The Problemist 2016).
|
|
|
Avant de chercher, peux-tu confirmer que R = Roi ?
|
|
|
@nicolasdupont
Pour les 12 coups
sur le cycle
a1 - b3 - c1
| |
c2 a2
| |
a3 - b1 - c3
les cavaliers Blancs sont placés en a3 b1 c3
les Noirs en a1 b3 c1
on choisit la case c2 ou a2 pour le premier mouvement et chaque cavalier doit faire 4 mouvements.
|
|
|
Oui R = Roi, et ce sont les noirs qui matent au septième coup.
|
|
|
i y a quelques années j'avais créé cette page pour ceux qui veulent s'essayer au parcours du cavalier d'Euler .
On peut visualiser le parcours en cliquant( maintenir) sur l'image(solution d'Euler) sous le plateau. cliquer sur une case de votre choix pour débuter... les cibles vertes sont disponibles, les rouges sont déjà utilisées.
pour revenir en arrière, cliquer sur le cavalier!
il y aurait 13 267 364 410 532 solutions
|
|
|
Ces problèmes me font penser aux rétros classiques qui contiennent des corridors de cavaliers. Il y a un excellent article en ligne à ce sujet (en anglais) : http://www.janko.at/Retros/KnightEvasionRoutes/
|
|
|



